Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiPhương pháp giải bài tập sự rơi tự do
1. DẠNG 1: TÍNH THỜI GIAN - QUÃNG ĐƯỜNG - VẬN TỐC. QUÃNG ĐƯỜNG VẬT ĐI ĐƯỢC TRONG ΔT GIÂY THỨ N. THỜI GIAN VẬT ĐI QUA M THỨ N
Phương pháp :
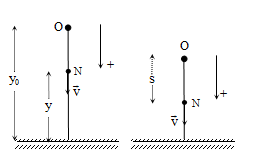
- Vẽ hình - Đánh dấu các vị trí khảo sát - ghi các đại lượng động học
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc bắt đầu rơi.
- Áp dụng các công thức:
\(\left\{ \begin{array}{l}s = \frac{1}{2}g{t^2}\\v = gt\\{v^2} = 2g{\rm{s}}\end{array} \right.\) và \(\Delta s = {s_n} - {s_{\left( {n - 1} \right)}} = \frac{1}{2}gt_n^2 - \frac{1}{2}g{\left( {{t_n} - 1} \right)^2}\)
2. DẠNG 2: LIÊN HỆ GIỮA QUÃNG ĐƯỜNG, THỜI GIAN, VẬN TỐC CỦA HAI VẬT RƠI TỰ DO
Phương pháp :
- Vẽ hình - Đánh dấu các vị trí khảo sát của 2 vật - ghi các đại lượng động học.
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc vật bắt đầu rơi.
Nếu gốc thời gian không trùng lúc vật bắt đầu rơi thì \({t_0} \ne 0\)
- Áp dụng các công thức cho 2 vật:
\(s = \frac{1}{2}g{t^2}{\rm{; }}v = gt;{\rm{ }}{v^2} = 2g{\rm{s; }}y = {y_0} + \frac{1}{2}g{t^2}\)
3. DẠNG 3: CHUYỂN ĐỘNG CỦA VẬT ĐƯỢC NÉM THẲNG ĐỨNG HƯỚNG XUỐNG
Phương pháp :
- Chuyển động có :
+ Gia tốc : \(\vec a\) = \(\vec g\)
+ Vận tốc đầu : \({\vec v_0}\)cùng phương với \(\vec a\)
+ Phương trình : y = \(\frac{1}{2}\) gt2 + v0t+y0 (Chiều dương hướng xuống)
- Vẽ hình
- Đánh dấu các vị trí khảo sát của 2 vật - ghi các đại lượng động học.
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc vật bắt đầu ném.
Nếu gốc thời gian không trùng lúc vật bắt đầu rơi thì \({t_0} \ne 0\)
- Áp dụng các công thức cho 2 vật:
\(\begin{array}{l}s{\rm{ }} = \frac{1}{2}g{t^2} + {v_0}t\\v{\rm{ }} = {\rm{ }}gt{\rm{ }} + {v_0}t\\{v^2}-{v_0}^2 = {\rm{ }}2gs\\y = {y_0} + \frac{1}{2}g{t^2} + {v_0}t\end{array}\)