Phương pháp giả các dạng bài tập chuyển động thẳng biến đổi đều

Các dạng bài tập chuyển động thẳng biến đổi đều MÔN LÝ Lớp 10 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(395) 1315 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I- DẠNG 1: XÁC ĐỊNH CÁC ĐẠI LƯỢNG: QUÃNG ĐƯỜNG - VẬN TỐC - GIA TỐC

    Phương pháp:

    + Chọn hệ quy chiếu

    + Áp dụng các công thức: \(\left\{ \begin{array}{l}x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\\v = {v_0} + at\end{array} \right.\) 

    • Vận tốc nhận giá trị dương nếu vật chuyển động cùng chiều dương, nhận giá trị âm nếu vật chuyển động ngược chiều dương.
    • Vật chuyển động nhanh dần đều thì a.v > 0, vật chuyển động chậm dần đều thì a.v < 0
    • Trong hệ đơn vị SI thì: s(m); v(m/s); a(m/s2) và \(1km/h = \frac{1}{{3,6}}m/s\)

    II- DẠNG 2: VIẾT PHƯƠNG TRÌNH CHUYỂN ĐỘNG

    Phương pháp:

    - Bước 1: Chọn hệ quy chiếu

         + Chọn trục tọa độ Ox

         + Chọn mốc thời gian t = 0
    - Bước 2: Viết phương trình chuyển động

    \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)

         + \({x_0}\): là tọa độ ban đầu của chất điểm (\({x_0}\)lấy giá trị dương nếu chất điểm nằm ở phía dương của trục tọa độ ấy, lấy giá trị âm nếu chất điểm nằm ở phía âm của trục tọa độ ấy)

         + v0: vận tốc của vật tại thời điểm ban đầu (t = 0)  (v0 lấy giá trị dương nếu chất điểm chuyển động cùng chiều dương và lấy giá trị âm nếu chất điểm chuyển động ngược chiều dương)

         + Vật chuyển động nhanh dần đều thì av > 0, chuyển động chậm dần đều thì av < 0.

                + t: thời gian chuyển động

    III- DẠNG 3: ĐỒ THỊ CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU

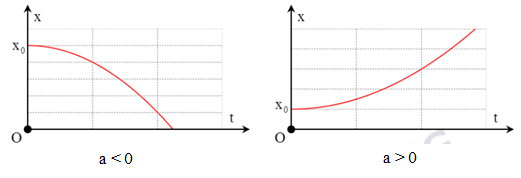
    1. Đồ thị tọa độ theo thời gian (x - t)

    Là nhánh parabol

    2. Đồ thị vận tốc theo thời gian (v - t)

    Là đường thẳng xiên góc.

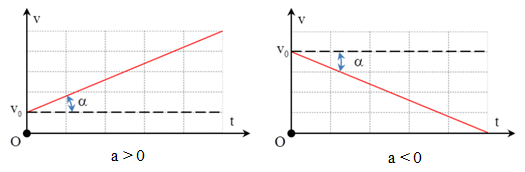
    Hệ số góc của đường biểu diễn v - t bằng gia tốc của chuyển động: \(a = \tan \alpha  = \frac{{v - {v_0}}}{t}\)

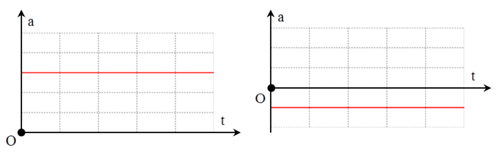
    3. Đồ thị gia tốc theo thời gian (a - t)

    Là đường thẳng song song với trục Ot

    Xem toàn bộ nội dung Vật lý 10:

    (395) 1315 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 10 Vật lý 10