Chuyển động thẳng biến đổi đều

Lý thuyết Chuyển động thẳng biến đổi đều, định nghĩa về chuyển động thẳng nhanh dần đều và chậm dần đều, các phương trình gia tốc, tọa độ, vận tốc và hệ thức độc lập thời gian trong chuyển động biến đổi đều, đồ thị x - t, v - t, a - t của chuyển động biến đổi đều.
(394) 1314 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I - CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU

    1. Định nghĩa

    Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi

    2. Các phương trình của chuyển động thẳng biến đổi đều

    - Gia tốc:

    \(\overrightarrow a  = \dfrac{{\overrightarrow v  - \overrightarrow {{v_0}} }}{{\Delta t}}\) có độ lớn: \(a = \dfrac{{v - {v_0}}}{{\Delta t}}\)

    - Phương trình tọa độ - thời gian của chuyển động thẳng biến đổi đều

    \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)

    Trong đó:

         + x­0 : tọa độ ban đầu của chất điểm

         + v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)

         + t: thời gian chuyển động

    - Phương trình vận tốc:

    \(v = {v_0} + at\)

    Trong đó:

         + v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)

         + a: gia tốc

         + t: thời gian chuyển động

    - Hệ thức độc lập thời gian:

    \({v^2} - v_0^2 = 2{\rm{a}}\Delta {\rm{x}}\)

    \((\Delta x = x - {x_0})\) là độ dời trong khoảng thời gian từ 0 đến t

    II- ĐỒ THỊ CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU

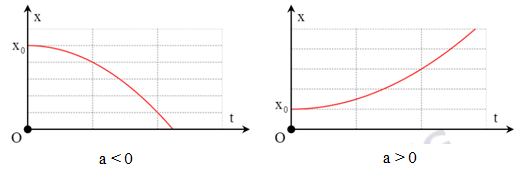
    1. Đồ thị tọa độ theo thời gian (x - t)

    Là nhánh parabol

    2. Đồ thị vận tốc theo thời gian (v - t)

    Là đường thẳng xiên góc.

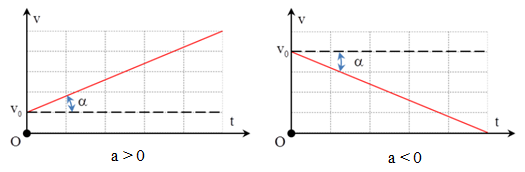
    Hệ số góc của đường biểu diễn v - t bằng gia tốc của chuyển động: \(a = \tan \alpha  = \frac{{v - {v_0}}}{t}\)

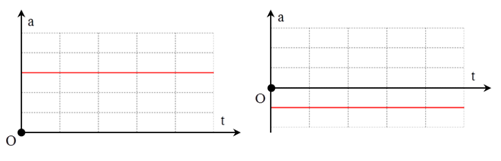
    3. Đồ thị gia tốc theo thời gian (a - t)

    Là đường thẳng song song với trục Ot

    Xem toàn bộ nội dung Vật lý 10:

    (394) 1314 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 10 Vật lý 10