Tần số góc của dao động điện từ tự do được xác định bằng biểu thức: \(\omega  = \frac{1}{{\sqrt {LC} }}\)

Đáp án cần chọn là: D

Nguyên tử hyđro đang ở trạng thái cơ bản, khi nhận được năng lượng kích thích thì bán kính quỹ đạo của electron tăng lên 16 lần, tức là:

 \({r_n} = {n^2}.{r_0} = 16{r_0} \Rightarrow n = 4\)

Khi chuyển từ mức năng lượng này sang mức năng lượng khác thì nguyên tử phát ra một photon có năng lượng thỏa mãn:

\(\begin{array}{l}\varepsilon  = \frac{{hc}}{\lambda } = {E_n} - {E_0} = \frac{{ - 13,6}}{{16}} - ( - 13,6) = 12,75eV = 20,{4.10^{ - 19}}J\\ \Rightarrow \lambda  = \frac{{hc}}{\varepsilon } = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{20,{{4.10}^{ - 19}}}} = 0,{974.10^{ - 7}}m = 0,0974\mu m\end{array}\)

Chọn B.

Công thức khoảng vân: \(i = \frac{{\lambda D}}{a} \Rightarrow i \sim \lambda \)

Bảng bước sóng ánh sáng:

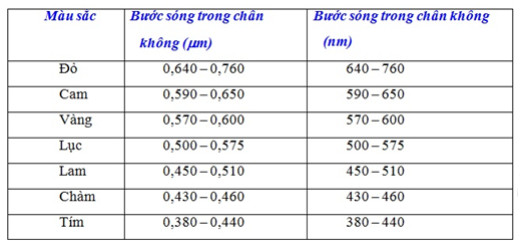
Nếu thay ánh sáng đơn sắc màu lục bằng ánh sáng đơn sắc màu vàng và giữ nguyên các điều kiện khác thì bước sóng tăng lên, nên khoảng vân tăng.

Chọn B. 

Toạ độ của vân sáng bậc 5 là: \({x_{s5}} = 5.i\)

Khoảng cách từ vân sáng bậc 5 đến vân sáng bậc 5 ở hai phía vân trung tâm là:

\(d = 5i + 5i = 10i = 10.\frac{{\lambda D}}{a} = 10.\frac{{0,6.2}}{1} = {12_{}}mm\)

Chọn C.

Thứ tự bước sóng giảm dần là: sóng vô tuyến, tia hồng ngoại, ánh sáng thấy được, tia X, tia gamma.

Chọn D.

Bán kính quỹ đạo xác định theo công thức:

\({r_n} = {n^2}.{r_0};\,\,\,n = 1,2,3,...\)

→ Vì vậy không thể có bán kĩnh quỹ đạo: \({r_n} = 8{r_0}\)

Chọn D.

Đổi đơn vị \(1eV = 1,{6.10^{ - 19}}J\)

Giới hạn quang điện của kim loại này là:

\({\lambda _0} = \dfrac{{hc}}{A} = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{4,14.1,{{6.10}^{ - 19}}}} = 3,{0.10^{ - 7}} = 0,3\mu m\)

Chọn C.

Đặc điểm quan trọng của quang phổ liên tục là không phụ thuộc vào thành phần cấu tạo mà chỉ phụ thuộc vào nhiệt độ của nguồn sáng.

Chọn B.

Phương trình phóng xạ:  \({}_{11}^{24}Na \to {}_{ - 1}^0e + {}_{12}^{24}Mg\)

Số hạt nhân ban đầu: \({N_0} = \frac{m}{A}.{N_A} = \frac{{12}}{{24}}.6,{023.10^{23}} = 3,{0115.10^{23}}\)

Số hạt nhân con được tạo thành sau thời gian t = 3T:

\(N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 3,{0115.10^{23}}.\left( {1 - {2^{\frac{{ - 3T}}{T}}}} \right) = 2,{626.10^{23}}\)

Chọn D. 

Phản ứng phân hạch là sự vỡ của một hạt nhân nặng thành hai hạt nhân trung bình (kèm theo một vài nơtron). Phân hạch là phản ứng tỏa năng lượng, phản ứng phân hạc có dây chuyển có thể điều khiển được tạo ra trong lò phản ứng hạt nhân.

Phản ưng nhiệt hạch là sự tổng hợp hai hay nhiều hạt nhân nhẹ thành một hạt nhân nặng hơn. Phản ứng xảy ra ở nhiệt độ cao và tỏa ra năng lượng rất lớn, là phản ứng không điều khiển được.

→ Điểm giống nhau của phản ứng phân hạch và nhiệt hạch là các phản ứng tỏa năng lượng (nhiệt).

Chọn D.

Các dạng phóng xạ :

+ phóng xạ α: \({}_Z^AX \to {}_2^4He + {}_{Z - 2}^{A - 4}Y\)

+ Phóng xạ β+: \({}_Z^AX \to {}_{Z - 1}^AY + {}_{ + 1}^0e\)

+ phóng xạ β-: \({}_Z^AX \to {}_{Z + 1}^AY + {}_{ - 1}^0e\)

+ Phóng xạ γ: không biến đổi hạt nhân, nó xuất hiện trong các phóng xạ β+ hoặc β- khi hạt nhân con ở trạng thái kích thích.

Chọn B.

Tia laze có tính đơn sắc, tính định hướng và tính kết hợp rất cao và cường độ lớn.

Trong công nghiệp, vì tia laze có cường độ lớn và tính định hướng cao nên nó được dùng trong các công việc như cắt, khoan, tôi... chính xác.

Chọn C.

Sử dụng định luật bảo toàn điện tích và bảo toàn nuclon ta có phương trình phản ứng:

\({}_3^6Li + {}_1^2H \to {}_4^7Be + {}_0^1n\)

→ Vậy hạt nhân X là: \({}_1^2H\)

Chọn B.

Bề rộng 6 vân sáng ứng với 5 khoảng vân. Nên ta có:

\(5i = 4,8mm \Rightarrow i = \frac{{4,8}}{5} = 0,96mm\)

Lại có: \(i = \frac{{\lambda D}}{a} \Rightarrow \lambda  = \frac{{ia}}{D} = \frac{{0,96.1}}{2} = 0,48\mu m\)

→ Tần số ánh sáng: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{0,{{48.10}^{ - 6}}}} = 6,{25.10^{14}}Hz\)

Chọn C.

Phương trình phóng xạ: \({}_{84}^{210}Po \to {}_{82}^{206}Pb + {}_2^4He\)

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\dfrac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành sau thời gian t được xác định bởi:

\(N' = {N_0} - N = {N_0}.(1 - {2^{\dfrac{{ - t}}{T}}})\)

Tại thời điểm t1 tỉ số giữa hạt nhân Poloni và hạt nhân chì có trong mẫu là \(\dfrac{1}{7}\) ta có:

\(\dfrac{{{N_{Po}}}}{{{N_{Pb}}}} = \dfrac{{{2^{\dfrac{{ - {t_1}}}{T}}}}}{{1 - {2^{\dfrac{{ - {t_1}}}{T}}}}} = \dfrac{1}{7} \Rightarrow {t_1} = 3T\)

Tại thời điểm \({t_2} = {t_1} + \Delta t\) thì tỉ số đó là \(\dfrac{1}{{31}}\) ta có :

\(\begin{array}{l}\dfrac{{{N_{Po}}}}{{{N_{Pb}}}} = \dfrac{{{2^{\dfrac{{ - ({t_1} + \Delta t)}}{T}}}}}{{1 - {2^{^{\dfrac{{ - ({t_1} + \Delta t)}}{T}}}}}} = \dfrac{1}{{31}} \Rightarrow \dfrac{{{2^{\dfrac{{ - {t_1}}}{T}}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}}{{1 - {2^{\dfrac{{ - {t_1}}}{T}}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}} = \dfrac{{{2^{ - 3}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}}{{1 - {2^{ - 3}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}} = \dfrac{1}{{31}}\\ \Rightarrow {31.2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} = 1 - {2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} \Rightarrow {32.2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} = 1\\ \Rightarrow {2^{\dfrac{{ - \Delta t}}{T}}} = \dfrac{1}{4} = {2^{ - 2}} \Rightarrow \Delta t = 2T = 276\,\,\left( {ngay} \right)\end{array}\)

Chọn A.

Công dụng của tia tử ngoại:

+ Tiệt trùng dụng cụ y tế, chữa bệnh còi xương.

+ Tiệt trùng thực phẩm đóng hộp.

+ Tìm vết nứt trên bề mặt kim loại.

→ Tia tử ngoại không được dùng để ứng dụng trong các bộ điều khiển từ xa của tivi, quạt, máy lạnh.

Chọn C.

Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)

Vì hai ánh sáng cùng cho các vân sáng, nên vị trí hai vân sáng trùng nhau thỏa mãn :

\(\begin{array}{l}x = k.\frac{{{\lambda _1}.D}}{a} = k'.\frac{{{\lambda _2}.D}}{a} \Rightarrow \frac{{{i_1}}}{{{i_2}}} = \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{k'}}{k}\\ \Rightarrow \frac{i}{{i'}} = \frac{{0,4}}{{0,6}} = \frac{2}{3} \Rightarrow {i_{tr}} = 2{i_2} = 3{i_1}\end{array}\)

Vân sáng bậc 7 của bức xạ λ₁ có vị trí: x_s7 = 7i₁

Vậy trong khoảng này có các cặp trùng nhau là: 

\(\left( {0;0} \right);\left( { \pm 2{i_2}; \pm 3{i_1}} \right);\left( { \pm 4{i_2}; \pm 6{i_1}} \right)\)

Vậy có 5 vân trùng nhau.

Chọn D.

Thuyết lượng tử ánh sáng

+ Chùm ánh sáng là chùm các phôtôn (các lượng tử ánh sáng). Mỗi phôtôn có năng lượng xác định (năng lượng của 1 phô tôn:

+ Cường độ chùm sáng tỉ lệ với số phôtôn phát ra trong 1 giây.

+ Phân tử, nguyên tử, electron… phát xạ hay hấp thụ ánh sáng,  nghĩa là chúng phát xạ hay hấp thụ phôtôn.

+ Các phôtôn bay dọc theo tia sáng với tốc độ c = 3.108 m/s trong chân không.

+ Năng lượng của mỗi phôtôn rất nhỏ. Một chùm sáng dù yếu cũng chứa rất nhiều phôtôn do rất nhiều nguyên tử, phân tử phát ra. Vì vậy ta nhìn thấy chùm sáng liên tục.

+ Phôtôn chỉ tồn tại trong trạng thái chuyển động. Không có phôtôn đứng yên.

→ Phát biểu đúng là: Với mỗi ánh sáng đơn sắc có tần số f, các phôtôn đều mang năng lượng như nhau

Chọn A.

Hiệu điện thế giữa Anot và Katot gia tốc cho electron, coi vận tốc đầu bằng 0, nên đến khi electron đập vào atot thì nó có năng lượng:

\[{{\rm{W}}_d} = \frac{1}{2}m.v_{\max }^2 = eU\]

Khi toàn bộ năng lượng này khi đập vào atot làm nó phát ra tia X có năng lượng lớn nhất ta có:

\(\begin{array}{l}hf = \frac{1}{2}.m.v_{\max }^2 = eU\\ \Rightarrow f = \frac{{eU}}{h} = \frac{{1,{{6.10}^{ - 19}}{{.30.10}^3}}}{{6,{{625.10}^{ - 34}}}} = 7,{245.10^{18}}Hz\end{array}\)

Chọn B.

Công thức khoảng vân \(i = \frac{{\lambda D}}{a} = \frac{{0,64.1}}{{0,4}} = 1,6mm\)

Ta có: \(\frac{x}{i} = \frac{{5,6}}{{1,6}} = 3,5 = 3 + \frac{1}{2} \Rightarrow k = 3\)

→ Tại M là vân tối thứ 4.

Chọn C.

Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)

Vì ba ánh sáng cùng cho các vân sáng, nên vị trí ba vân sáng trùng nhau thỏa mãn :\(\begin{array}{l}x = {k_1}.\frac{{{\lambda _1}.D}}{a} = {k_2}.\frac{{{\lambda _2}.D}}{a} = {k_3}.\frac{{{\lambda _3}.D}}{a}\\ \Rightarrow {i_1}:{i_2}:{i_3} = {\lambda _1}:{\lambda _2}:{\lambda _3} = a:b:c = 0,4:0,5:0,6 = 4:5:6\end{array}\)

Ta xét vân trung tâm và vân trùng 3 màu đầu tiên, ứng với vị trí:

\[x = 15{i_1} = 12{i_2} = 10{i_3}\]

Vị trí trùng nhau của hai bước sóng λ1 và λ2 có khoảng vân trùng cặp 12 là:

\({i_{12}} = 5{i_1} = 4{i_2}\)

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ1 và λ2 là:

 (15:5)-1=2

Vị trí trùng nhau của hai bước sóng λ1 và λ3 có khoảng vân trùng cặp 13 là:

 \({i_{13}} = 3{i_1} = 2{i_3}\) 

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ1 và λ3 là:

 (15:3)-1=4

Vị trí trùng nhau của hai bước sóng λ2 và λ3 có khoảng vân trùng cặp 23 là:

\({i_{23}} = 6{i_2} = 5{i_3}\)

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ2 và λ3là:

 (12:6)-1=1 

Vậy số vị trí chỉ có 1 vạch màu đơn sắc là :

\((15 + 12 + 10) - (1.3 + 2.2 + 2.4 + 2.1) = 20\)

Chọn B.

Công suất phát: \(P = N.\varepsilon  = N.hf\)

Suy ra: \(N = \dfrac{P}{{hf}} = \dfrac{{0,4}}{{6,{{625.10}^{ - 34}}.7,{{5.10}^{14}}}}\)

\(= 8,{05.10^{17}}\) 

Chọn C.

Lực tương tác giữa êlectron và hạt nhân của nguyên tử Hidro trên quỹ đạo K là :

 \(F = k.\frac{{|{q_e}.{q_p}|}}{{{r_0}^2}}\)

Lực tương tác giữa êlectron và hạt nhân của nguyên tử Hidro trên quỹ đạo M là :

\({F_M} = k.\frac{{|{q_e}.{q_p}|}}{{{{\left( {{3^2}{r_0}} \right)}^2}}} = k.\frac{{|{q_e}.{q_p}|}}{{81{r_0}^2}} = \frac{F}{{81}}\)

Chọn C.

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:

\(\begin{array}{l}N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 70\% {N_0}\\ \Rightarrow (1 - {2^{\frac{{ - t}}{T}}}) = 70\%  = 0,7 \Rightarrow {2^{\frac{{ - t}}{T}}} = 0,3\\ \Rightarrow t =  - T.{\log _2}(0,3) = 1,74T = 1,74.3,8 = 6,6\end{array}\)

Vậy thời gian là 6,6 ngày.

Chọn A.

Độ hụt khối của hạt nhân \({}_4^{10}Be\) là:

\(\begin{array}{l}\Delta m = \left[ {Z.{m_p} + \left( {A - Z} \right).{m_n}} \right] - {m_X}\\ \Rightarrow \Delta m = \left[ {4.1,0073 + (10 - 4).1,0087} \right] - 10,0113 = 0,0701u\end{array}\)

Chọn B. 

Chu kì dao động của con lắc lò xo: \(T=2\pi \sqrt{\frac{m}{k}}\) 

Chọn D.

\(\begin{align}& x=4\sqrt{2}\angle \dfrac{\pi }{3}+4\sqrt{2}\angle -\frac{\pi }{6}=8\angle \dfrac{\pi }{12} \\& \Rightarrow x=8cos\left( 10\pi t+\dfrac{\pi }{12} \right)cm \\\end{align}\)

Chọn A.

Ta có điều kiện của biên độ tổng hợp của hai dao động thành phần: \(\left| {{A}_{1}}-{{A}_{2}} \right|\le A\le {{A}_{1}}+{{A}_{2}}\)

Chọn D.

Gọi:

- Khoảng cách từ tâm chấn động đến nơi nhận tín hiệu là \(S\)

- Thời gian nhận được tín hiệu thứ nhất (sóng ngang) là \({{t}_{1}}\)

- Thời gian nhận được tín hiệu thứ 2 (sóng dọc) là \({{t}_{2}}\)

Ta có:

+ Thời gian tín hiệu truyền đến trong lòng đất với sóng ngang là: \({{t}_{1}}=\frac{S}{{{v}_{1}}}=\frac{S}{5}\)

+ Thời gian tín hiệu truyền đến trong lòng đất với sóng dọc là: \({{t}_{2}}=\frac{S}{{{v}_{2}}}=\frac{S}{8}\)

Lại có:

\({{t}_{2}}-{{t}_{1}}=270s\Leftrightarrow \frac{S}{5}-\frac{S}{8}=270\)

\(\Rightarrow S=3600km\)

Chọn D.

Khoảng cách giữa hai điểm gần nhất trên cùng một phương truyền sóng dao động cùng pha chính là một bước sóng .

Chọn B.

Cường độ âm I tại một điểm là đại lượng đo bằng năng lượng mà sóng âm tải qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian:

\(I=\dfrac{P}{S}\)

Đơn vị: \(\text{W}/{{m}^{2}}\)

Chọn B.

A – đúng.

B – sai vì dao động của con lắc lò xo có thể là dao động tắt dần, duy trì, cưỡng bức, …

C – sai vì dao động của con lắc đơn có thể là dao động tắt dần, duy trì, cưỡng bức, …

D – sai vì cơ năng của vật dao động điều hòa tỉ lệ thuận với bình phương biên độ dao động.

Chọn A. 

Ta có:

+ Biên độ dao động của vật: \(A=20mm=2cm\)

+ Tần số góc của dao động: \(\omega =2\pi f=2\pi .2=4\pi \left( rad/s \right)\)

+ Tại thời điểm ban đầu\(t=0\),

\(\left\{ \begin{array}{l}{x_0} = Acos\varphi  = 1cm\\v =  - Asin\varphi  < 0\end{array} \right.\)

\(\Rightarrow \left\{ \begin{array}{l}cos\varphi  = \frac{1}{2}\\\sin \varphi  > 0\end{array} \right. \Rightarrow \varphi  = \frac{\pi }{3}\) 

+ Phương trình dao động của vật: \(x=2cos\left( 4\pi t+\frac{\pi }{3} \right)cm\)

Chọn B.

Ta có, tổng trở của mạch RLC mắc nối tiếp: \(Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\)

Lại có: \(\left\{ \begin{align}& {{Z}_{L}}=\omega L \\& {{Z}_{C}}=\frac{1}{\omega C} \\\end{align} \right.\)

\(\Rightarrow Z=\sqrt{{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\)

Chọn D.

+ Tần số của sóng: \(f=\dfrac{\omega }{2\pi }=\dfrac{30\pi }{2\pi }=15Hz\)

+ Bước sóng: \(\lambda =\dfrac{v}{f}=\dfrac{60}{15}=4cm\)

+ Điểm P có:  \(PA-PB=6cm=\dfrac{3}{2}\lambda \)

\(\Rightarrow P\) thuộc cực tiểu số 2 tính từ trung trực AB đi ra

Điểm Q có: \(QA-QB=12cm=3\lambda \)

\(\Rightarrow Q\) thuộc cực đại số 3 tính từ trung trực AB đi ra

Chọn A. 

Sóng dừng trên dây 2 đầu cố định: \(l=k\dfrac{\lambda }{2}\) (1)

Lại có 5 nút sóng \(\Rightarrow k=5-1=4\)

Thay vào (1) ta được: \(1=4\dfrac{\lambda }{2}\Rightarrow \lambda =0,5m\)

Chọn B.

 Ta có: \(\Delta t = \frac{{4T}}{3} = T + \dfrac{T}{3}\)

\( \Rightarrow \) Quãng đường vật đi được: \(S = {S_T} + {S_{\max \left( {\dfrac{T}{3}} \right)}}\)

Ta có:

+ \({S_T} = 4A\)

+ Quãng đường lớn nhất vật đi được trong khoảng thời gian \(\dfrac{T}{3}\) : \({S_{max}} = 2A\sin \dfrac{{\Delta \varphi }}{2}\)

Ta có: \(\Delta \varphi  = \omega \Delta t = \dfrac{{2\pi }}{T}.\frac{T}{3} = \dfrac{{2\pi }}{3}\)

\( \Rightarrow {S_{\max }} = 2A\sin \dfrac{{\dfrac{{2\pi }}{3}}}{2} = \sqrt 3 A\)

\( \Rightarrow \) Quãng đường lướn nhất mà vật đi được trong khoảng thời gian \(\Delta t = \dfrac{{4T}}{3}\) là: \(S = 4A + \sqrt 3 A\) 

Chọn C.

Ta có:

+ Biên độ dao động của vật: \(A = 3cm\)

+ Chu kì dao động của vật: \(T = \dfrac{{20}}{{50}} = 0,4s\)

+ Độ dãn của lò xo tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{g{T^2}}}{{4{\pi ^2}}} = \dfrac{{10.0,{4^2}}}{{4.10}} \)

\(= 0,04m= 4cm\)

Lực đàn hồi cực đại tại vị trí thấp nhất: \({F_{dhMax}} = k\left( {\Delta l + A} \right)\)  (1)

Nhận thấy \(\Delta l > A\) \( \Rightarrow {F_{dhMin}} = k\left( {\Delta l - A} \right)\) (2)

Từ (1) và (2), ta suy ra: \(\dfrac{{{F_{dhMax}}}}{{{F_{dhMin}}}} = \dfrac{{k\left( {\Delta l + A} \right)}}{{k\left( {\Delta l - A} \right)}} = \dfrac{{\Delta l + A}}{{\Delta l - A}} \)

\(= \dfrac{{4 + 3}}{{4 - 3}} = 7\)

Chọn A.

Ta có chu kì \(T = 2\pi \sqrt {\dfrac{l}{g}} \)

\( \Rightarrow \) Gia tốc rơi tự do: \(g = \dfrac{{4{\pi ^2}l}}{{{T^2}}}\)

+ Giá trị trung bình của gia tốc trọng trường: \(\overline g  = \dfrac{{4{\pi ^2}\overline l }}{{{{\overline T }^2}}} = \dfrac{{4{\pi ^2}.1}}{{{2^2}}} = 9,87m/{s^2}\)

+ Sai số:

\({l}\dfrac{{\Delta g}}{{\overline g }} = \dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }}\)

\(\Rightarrow \Delta g = \left( {\dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }}} \right)\overline g \\ \Rightarrow \Delta g = \left( {\dfrac{1}{{100}} + 2\dfrac{{0,01}}{2}} \right)9,87\)

\(= 0,1974 \approx 0,2m/{s^2}\)

\( \Rightarrow g = \overline g  \pm \Delta g = 9,87 \pm 0,2{\rm{ m/}}{{\rm{s}}^2}\)

Chọn C.

+ Ta có, vật có vận tốc bằng 0 khi ở vị trí biên

+ Khoảng thời gian giữa 2 lần liên tiếp vật có vận tốc bằng 0 là \(\frac{T}{2}\)

\( \Rightarrow {t_2} - {t_1} = \frac{T}{2} \Leftrightarrow 2,9 - 2,2 = \frac{T}{2} \Rightarrow T = 1,4s\)

+ Khoảng thời gian từ \({t_0} = 0s\) đến \({t_2} = 2,9s\) là:

 \(\Delta t = 2,9 - 0 = 2,9s = 2T + \frac{T}{{14}}\)

Trong 1 chu kì vật qua VTCB 2 lần

\( \Rightarrow \) Trong 2 chu kì vật qua VTCB 4 lần

Trong \(\frac{T}{{14}}\) vật qua VTCB 0 lần

\( \Rightarrow \) Trong khoảng thời gian từ \({t_0} = 0s\) đến \({t_2} = 2,9s\) vật qua VTCB 4 lần

Chọn B.