Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề thi HK1 môn Toán 6 năm 2020 - Trường THCS Trần Mai Ninh
-
Hocon247
-
30 câu hỏi
-
60 phút
-
67 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho tập B \(B = \left\{ {x \in N\left| {x \le 7} \right.} \right\}\). Liệt kê các phần tử của B?
B = {0;1; 2;3; 4;5; 6;7}
Chọn đáp án A
Cho tập \(D = \left\{ {x \in {N^*}\left| {x \le 6} \right.} \right\}\). Liệt kê các phần tử của D?
D = {1; 2;3; 4;5; 6}
Chọn đáp án A
Cho tập \(E = \left\{ {x \in N\left| {30 \le x \le 40;x \vdots 4} \right.} \right\}\). Liệt kê các phần tử của E?
Ta có: E = {32;36; 40}
Chọn đáp án A
Cho tập E = {4; 6; 8; 10} . Chỉ ra tính chất đặc trưng của các phần tử thuộc E ?
Ta có: \(E = \left\{ {x \in N\left| {x < 11;x \vdots 2} \right.} \right\}\)
Chọn đáp án B
Cho tập hai tập hợp A = {1; 2; 3; 4; 5; 6}; B = {1; 5; 7; 9} . Tập hợp E bao gồm các phần tử vừa thuộc A vừa thuộc B là?
Tập hợp E bao gồm các phần tử vừa thuộc A vừa thuộc B là E = {1;5}
Chọn đáp án C
Số các tập con có 2 phần của A={0; 2; 4; 6} là bao nhiêu?
Các tập con có 2 phần tử là: {0; 2};{0; 4};{0; 6};{2; 4};{2; 6};{4; 6}.
Chọn A.
Cho tập hợp A ={a, b, c, d , e}. Số tập con của A có 4 phần tử là bao nhiêu?
Các tập con có 4 phần tử là: {a;b; c; d};{a;b; c; e};{a;b; d; e};{b; c; d; e};{a; c; d; e}
Chọn đáp án D
Cho tập hợp C ={1; 2;3} . Cách viết nào sau đây là sai?
Kí hiệu \(\in \) dùng để chỉ mối quan hệ giữa tập hợp – phần tử,
Kí hiệu \(\subset \) dùng để biểu thị mối quan hệ giữa hai tập hợp. Chọn A.
Trong các tập sau đây, tập nào có đúng hai tập con?
Tập {a} có hai tập con là Ø; {a}
Chọn đáp án A
Cho các tập hợp : A = Ø; B = {1; 2}; C = {2, 3}; \(D = \left\{ {x \in N/1 < x < 3} \right\}\)
Cho các tập hợp : A = Ø; B = {1; 2}; C = {2, 3}; \(D = \left\{ {x \in N/1 < x < 3} \right\}\)
Khẳng định nào sau đây là sai?
Ta có: tập hợp C = {2, 3} mà A = Ø nên \(C \subset A\) là sai
Chọn đáp án C
Số tự nhiên liền trước của số tự nhiên x - 2 là bao nhiêu?
Số tự nhiên liền sau của số tự nhiên x - 2 là x - 2 -1 = x - 3 .
Chọn đáp án B.
Số phần tử của tập hợp các số tự nhiên chẵn lớn hơn 13 và nhỏ hơn 3000 là bao nhiêu?
Tập hợp các số tự nhiên chẵn lớn hơn 13 và nhỏ hơn 3000 là {14;16;18;...; 2996; 2998}
Có số phần tử là (2998 -14) : 2 +1 = 1493 phần tử.
Chọn đáp án A.
Từ nào sau đây có tập hợp các chữ cái gồm 5 phần tử?
Tập hợp các chữ cái trong từ “Song Hong” là {S, o, n, g, H}
Tập hợp các chữ cái trong từ “Song Me Kong” là {S, o, n, g, M , e, K}
Tập hợp các chữ cái trong từ “Song Sai Gon” là {S, o, n, g, a, i}
Tập hợp các chữ cái trong từ “Song Dong Nai” là {S, o, n, g, D, N , a, i}
Chọn đáp án A
Cho dãy số 1; 4;7;... , số hạng thứ 100 của dãy là bao nhiêu?
Gọi số hạng thứ 100 của dãy là x , ta có ( x -1) : 3 +1 = 100 Þ x = 298 .
Chọn đáp án A
Để đánh số trang của một cuốn sách (từ trang 1 đến hết), bạn Hà phải viết tất cả 282 chữ số. Hỏi cuốn sách đó có bao nhiêu trang?
99 trang đầu cần dùng 9.1+ 90.2 = 189 (chữ số)
999 trang đầu cần dùng 9.1+ 90.2 + 900.3 = 2889 (chữ số) Vì 189 < 282 < 2889 nên trang cuối cùng phải có 3 chữ số.
Số chữ số dùng để đánh số các trang có 3 chữ số là : 282 -189 = 93 (chữ số) Số trang có 3 chữ số là 93: 3 = 31 (trang)
Số trang của quyển sách là 99 + 31 =130 (trang)
Viết liên tiếp các số tự nhiên từ 1 đến 999 thành một hàng ngang, ta được số 123.... 999. Tổng các chữ số của số đó là bao nhiêu?
Viết liên tiếp các số tự nhiên từ 1 đến 99 ta được tổng các chữ số là:
10.(1+ 2 + 3 +... + 8 + 9) +10 + 20 + 30 +... + 80 + 90 = 450 + 450 = 900
Viết liên tiếp các số tự nhiên từ 100 đến 999 ta được tổng các chữ số là:
900 +100 + 200 + 300 +... + 800 + 900 = 5400
Vậy viết liên tiếp các số tự nhiên từ 1 đến 999 thành một hàng ngang, ta được số 123...999 thì tổng các chữ số của số đó là 900 + 5400 = 6300
Chọn đáp án B
Từ các số 1, 4,5, 7,8 có thể viết được bao nhiêu số tự nhiên có 3 chữ số khác nhau?
Gọi số tự nhiên có 3 chữ số cần tìm là abc
a: có 5 cách chọn.
b: có 4 cách chọn.
c: có 3 cách chọn. Vậy có 5.4.3 = 60 số.
Chọn đáp án A.
Với các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số?
Gọi số có 6 chữ số cần tìm là \(\overline {abcdef} \).
a : có 6 cách chọn.
b : có 6 cách chọn.
c : có 6 cách chọn.
d : có 6 cách chọn.
e : có 6 cách chọn.
f : có 6 cách chọn.
Nên có tất cả 6.6.6.6.6.6 = 46656 số.
Chọn đáp án D.
Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên có 5 chữ số?
Gọi số có 5 chữ số cần tìm là \(\overline {abcde}\)
a : có 5 cách chọn.
b : có 5 cách chọn.
c : có 5 cách chọn.
d : có 5 cách chọn.
e : có 5 cách chọn.
Nên có tất cả 5.5.5.5.5 = 3125 số. Chọn A.
Với 5 chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 2 chữ số?
Gọi số tự nhiên có 2 chữ số là ab .
a : có 5 cách chọn.
b : có 5 cách chọn.
Nên có tất cả 5.5 = 25 số.
Chọn đáp án A.
Đố vui:
“ Một con vịt bơi trước hai con vịt
Một con vịt bơi giữa hai con vịt
Một con vịt bơi sau hai con vịt”
Hỏi tổng cộng có bao nhiêu con vịt?
Với ba con vịt bơi thẳng hàng như hình sau thì cả ba khẳng định đều đúng:
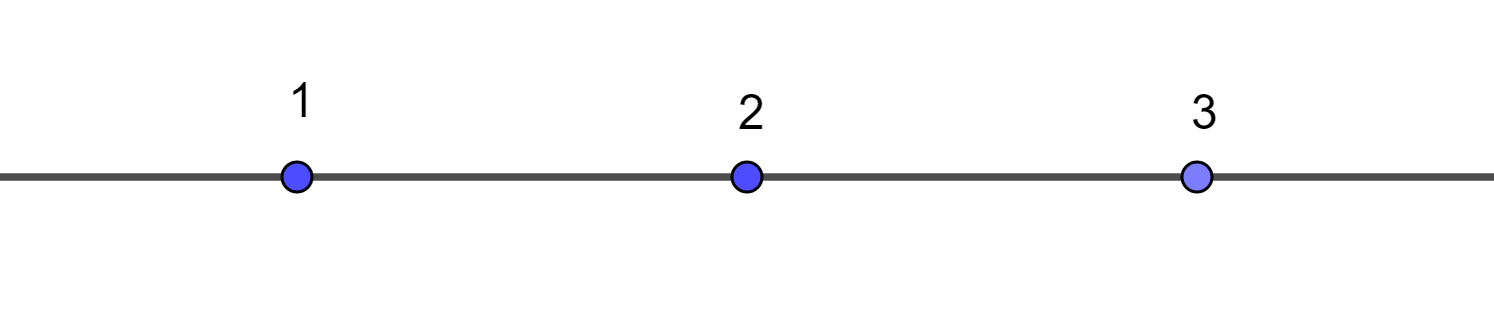
Con vịt 1 bơi trước hai con vịt 2 và 3
Con vịt 2 bơi giữa hai con vịt 1 và 3
Con vịt 3 bơi sau hai con vịt 1 và 2
Vậy có ba con vit
Chọn đáp án B
Cho ba điểm A, B, C thẳng hàng sao cho điểm A nằm giữa hai điểm B và C. Hình vẽ nào sau đây biểu diễn đúng?
Đáp án A: Điểm B nằm giữa A và C
Đáp án B: Điểm C nằm giữa A và B
Đáp án C: Điểm A nằm giữa B và C
Đáp án D: Điểm B nằm giữa A và C
Chọn đáp án C
Xem hình sau đọc tên các bộ ba điểm thẳng hàng với điểm I là điểm nằm giữa
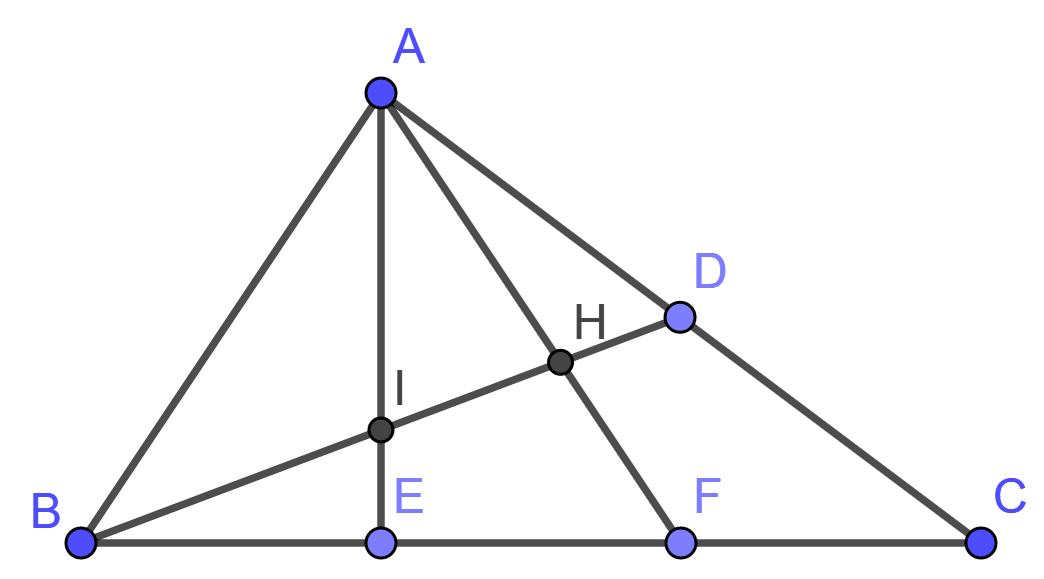
Bộ ba điểm thẳng hàng với I là điểm nằm giữa là: (A, I, E) và (B, I, H) và (B, I, D)
Chọn đáp án B
Trong hình sau có bao nhiêu bộ ba điểm thẳng hàng?
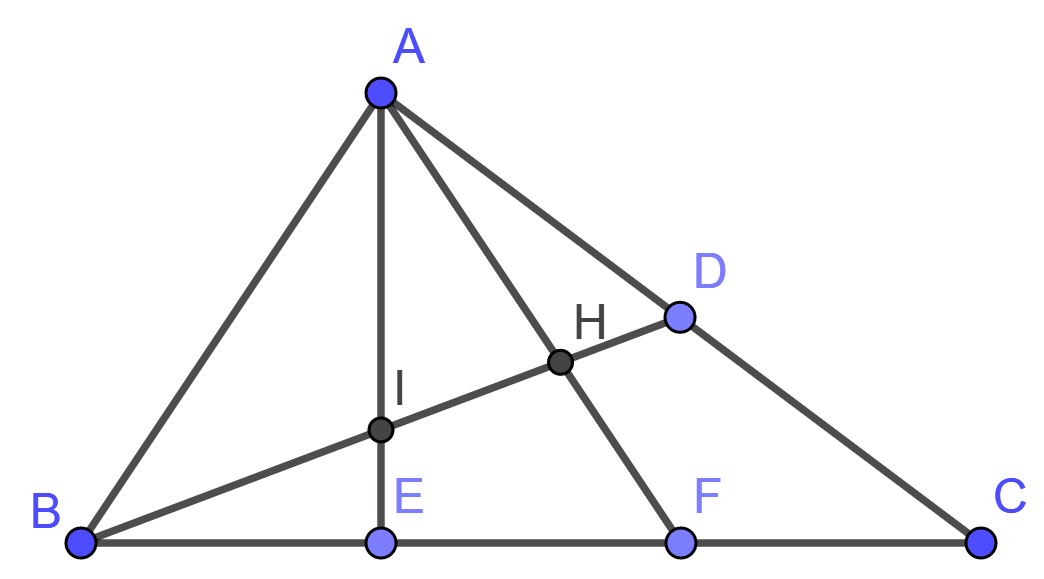
Bộ ba điểm thẳng hàng là:
( A, I, E), ( A, H, F), (A, D, C), (B, I, H), (B, I, D), (I, H, D), (B, E, F), (B, F, C), (E, F, C)
Vậy có tất cả 9 bộ ba điểm thẳng hàng
Chọn đáp án C
Cho hai đường thẳng a, b. Khi đó a, b có thể:
Hai đường thẳng a, b bất kỳ có thể trùng nhau, song song hoặc cắt nhau.
Chọn đáp án D.
Chọn câu đúng:
• Đáp án A: Qua hai điểm phân biệt có một và chỉ một đường thẳng nên A sai.
• Đáp án B: Có vô số điểm thuộc một đường thẳng nên B đúng.
• Đáp án C: Hai đường thẳng phân biệt thì có thể song song hoặc cắt nhau nên C sai.
• Đáp án D: Trong ba điểm thẳng hàng thì chỉ có một điểm nằm giữa hai điểm còn lại nên D sai.
Chọn đáp án B.
Cho ba điểm A; B; C không thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được những đường thẳng nào?
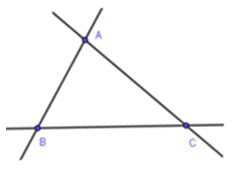
Các đường thẳng trong hình là: AB, BC, CA
Chọn đáp án A.
Cho 5 điểm A; B; C; D; E trong đó không có ba điểm nào thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng?
Các đường thẳng là: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE
Vậy có tất cả 10 đường thẳng cần tìm.
Chọn đáp án B.
Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
Ba đường thẳng đôi một không có giao điểm nghĩa là:
• a, b không có giao điểm hay a song song b.
• b, c không có giao điểm hay b song song c.
• a, c không có giao điểm hay a song song c.
Vậy ba đường thẳng đôi một song song.
Chọn đáp án C.
Cho bốn điểm M, N, P ,Q trong đó ba điểm M, N, P thẳng hàng và điểm Q nằm ngoài đường thẳng trên. Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng phân biệt?
Vì ba điểm M, N, P thẳng hàng nên qua hai điểm bất kì trong ba điểm trên ta đều nhận được một đường thẳng. Vậy từ ba điểm trên ta được một đường thẳng.
Các đường thẳng còn lại là: QM, QN, QP
Vậy có tất cả 4 đường thẳng phân biệt
Chọn đáp án B
.JPG)