Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề thi HK1 môn Toán 6 năm 2020 - Trường THCS Mỹ trung
-
Hocon247
-
30 câu hỏi
-
60 phút
-
65 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tập hợp \(A = \left\{ {x \in N\left| {8 < x < 14} \right|} \right\}\) gồm những phần tử nào?
A = {9;10;11;12;13}
Chọn đáp án D
Cho tập \(C = \left\{ {x \in N\left| {21 \le x \le 23} \right.} \right\}\).Liệt kê các phần tử của C?
C = {21; 22; 23}
Chọn đáp án C
Cho tập \(E = \left\{ {x \in N\left| {20 \le x \le 40;x \vdots 3} \right.} \right\}\). Liệt kê các phần tử của E ?
E = {21; 24; 27;30;33;36;39}
Chọn đáp án D
Cho tập E = {10; 11; 12; ...; 98; 99}. Chỉ ra tính chất đặc trưng của các phần tử thuộc E ?
\(E = \left\{ {x \in N\left| {9 < x < 100} \right.} \right\}\)
Chọ đáp án D
Cho tập A ={0; 2; 4; 6} . Số tập con của A là ?
Nếu tập A có n phần tử thì sẽ có 2n tập con. Vì tập A có 4 phần tử nên số tập con là
24 = 16 tập con.
Chọn đáp án A.
Số các tập con có 2 phần của A ={1; 2;3; 4;5; 6} là bao nhiêu?
Các tập con có 2 phần tử là:
{1; 2};{1;3};{1; 4};{1;5};{1; 6};{2;3};{2; 4};{2;5};
{2; 6};{3; 4};{3;5};{3; 6};{4;5};{4; 6};{5; 6}
Chọn đáp án C
Cho tập hợp A ={a, b, c, d , e}. Số tập con của A có 3 phần tử trong đó có chứa 2 phần tử a, b là?
Các tập con cần tìm là: {a;b; c};{a;b; d};{a;b; e} .
Chọn A.
Trong các tập sau đây, tập nào có đúng một tập con?
Các đáp án A, C, D đều có 2 tập con là Ø và chính nó. Tập Ø chỉ có 1 tập con chính là tập Ø. Chọn B
Cho tập A ={1; 2} và B ={1; 2;3; 4;5} . Có tất cả bao nhiêu tập X thỏa mãn \(A \subset X \subset B\) ?
Các tập X cần tìm là:
{1; 2};{1; 2;3};{1; 2; 4};{1; 2;5};{1; 2;3; 4};{1; 2;3;5};{1; 2; 4;5};{1; 2;3; 4;5}.
Chọn đáp án D
Cho tập hợp B gồm 100 số tự nhiên đầu tiên. Khẳng định nào sau đây đúng?
Tập B = {0;1; 2....... ;99}
Chọn đáp án B
Tập hợp các số tự nhiên nhỏ hơn hoặc bằng 6 được viết là:
Ta có: {0;1; 2;3; 4;5; 6}
Chọn đáp án C
Cho A = (1;3; a;b); B = (3;b) . Chọn khẳng định đúng?
Ta có a là 1 phần tử của A nên \(a \in A\)
Chọn đáp án A
Số các tập hợp X thoả mãn điều kiện: \(\left\{ {1;{\rm{ }}2;3} \right\}{\rm{ }} \subset X\; \subset \;\left\{ {1;{\rm{ }}2;3;{\rm{ }}4} \right\}\) là:
Tập X là: {1; 2;3};{1; 2;3; 4}
Chọn đáp án B
Cho hai tập hợp: A = {1; 2;3; 4;5; 6}; B = {1;3;5; 7;9} . Tập hợp gồm các phần tử thuộc A và không thuộc B là?
Ta có Tập hợp gồm các phần tử thuộc A và không thuộc B là {2; 4; 6}
Chọn đáp án D
Cho hai tập hợp A = {1; 2;3; 4;5; 6}; B = {1;3;5; 7;9} . Tập hợp gồm các phần tử thuộc B và không thuộc A là?
Ta có tập hợp gồm các phần tử thuộc B và không thuộc A là {7;9}
Chọn đáp án C
Số tự nhiên liền sau của số 999 là
Số tự nhiên liền sau của số 999 là 999 +1 = 1000 .
Chọn A
Số tự nhiên liền trước của số 25 là
Để tìm số tự nhiên liền trước của số tự nhiên a , ta tính a -1
Số tự nhiên liền sau của số 25 là 25 -1 = 24
Chọn A
Số tự nhiên liền trước của số tự nhiên m là
Số tự nhiên liền sau của số tự nhiên m là m -1.
Chọn đáp án A.
Số tự nhiên liền sau, liền trước của số 99 lần lượt là
Số tự nhiên liền sau của số 99 là 99 +1 =100
Số tự nhiên liền trước của số 99 là 99 -1 = 98 .
Chọn B.
Dùng kí hiệu để ghi lại cách diễn dạt sau: “Đường thẳng a chứa điểm M và không chứa điểm P. Điểm O thuộc đường thẳng a và không thuộc đường thẳng b”
Kí hiệu cho cách diễn đạt “Đường thẳng a chứa điểm M và không chứa điểm P. Điểm O thuộc đường thẳng a và không thuộc đường thẳng b” là: M ∈ a; P ∉ a; O ∈ a; O ∉ b.
Chọn đáp án A.
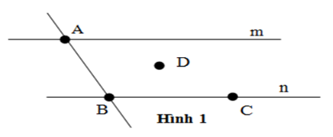
Cho hình vẽ sau:
Chọn câu sai:
Từ hình vẽ:
Điểm A ∈ m, A ∉ n nên A, B, D đúng và C sai.
Chọn đáp án C.
Trong các khẳng định sau, khẳng định đúng là khẳng định nào?
Một điểm có thể thuộc một, hai, ba, … đường thẳng. Do đó, đáp án A và B sai
Đường thẳng là tập hợp các điểm nên trên đường thẳng có vô số điểm. Đáp án C đúng
Một điểm cũng là một hình. Đáp án D sai
Chọn đáp án C
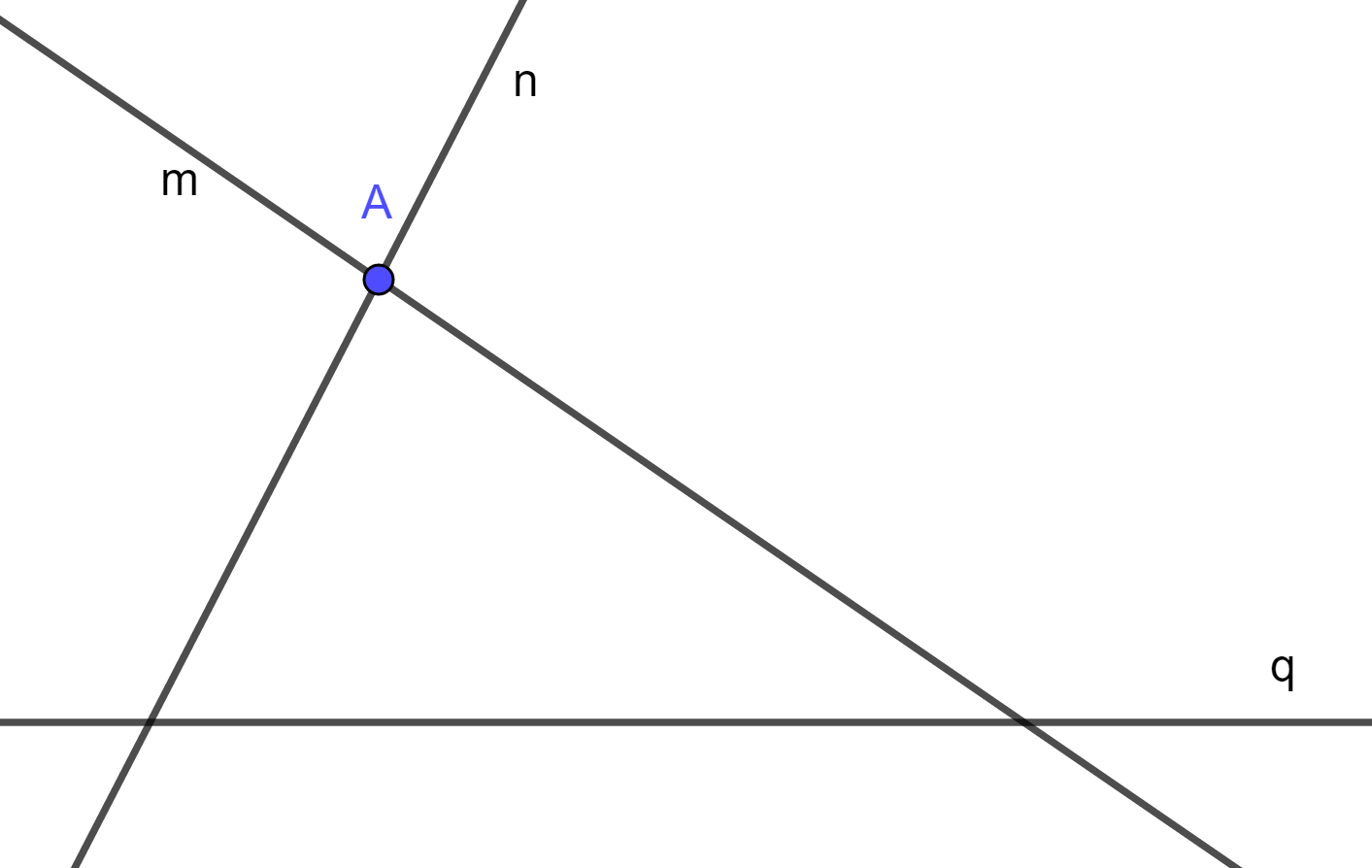
Cho hình vẽ sau, dùng kí hiệu để mô tả hình vẽ đó
Dựa vào hình vẽ ta thấy, điểm A thuộc đường thẳng m và n, điểm A không thuộc đường thẳng q
Chọn đáp án C
Chọn câu đúng:
Từ định nghĩa ba điểm thẳng hàng ta thấy đáp án C đúng.
Chọn đáp án C.
Cho ba điểm M; N; P thẳng hàng với P nằm giữa M và N. Chọn hình vẽ đúng:
• Đáp án A: Ta thấy ba điểm M; N; P thẳng hàng và điểm P nằm giữa hai điểm M, N nên A đúng.
• Đáp án B: Ta thấy ba điểm M; N; P thẳng hàng và điểm P không nằm giữa hai điểm M, N nên B sai.
• Đáp án C: Ta thấy ba điểm M; N; P không thẳng hàng nên C sai.
• Đáp án D: Ta thấy ba điểm M; N; P không thẳng hàng nên D sai.
Chọn đáp án A.
Kể tên bộ ba điểm thẳng hàng trong hình vẽ đưới đây:
.png)
Các bộ ba điểm thẳng hàng trong hình vẽ là: A, O, C và B, O, D
Chọn đáp án C.
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ sau:
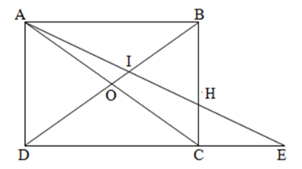
Các bộ ba điểm thẳng hàng trong hình vẽ là:
(A, O, C), (B, O, D), (D, C, E), (B, H, C), (A, I, H), (A, I, E), (A, H, E), (I, H, E), (D, O, I), (D, I, B), (O, I, B)
Vậy có tất cả 11 bộ ba điểm thẳng hàng trong hình vẽ.
Chọn đáp án B.
Cho hình vẽ sau. Chọn câu sai:
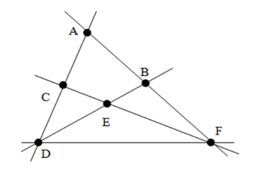
• Đáp án A: Ba điểm D; E; B thẳng hàng nên A đúng.
• Đáp án B: Ba điểm C; E; A không thẳng hàng nên B đúng.
• Đáp án C: Ba điểm A; B; F thẳng hàng nên C đúng.
• Đáp án D: Ba điểm D; E; F không thẳng hàng nên D sai.
Chọn đáp án D.
Trong các khẳng định sau, khẳng định nào đúng?
Ba điểm phân biệt có thể không thẳng hàng do đó đáp án A sai
Ba điểm phân biệt không thẳng hàng thì không tồn tại điểm nằm giữa hai điểm còn lại nên đáp án B sai
Với ba điểm A, B, C thẳng hàng thì ta có thể vẽ được bất kì một trong ba điểm nằm giữa hai điểm còn lại. Do đó, đáp án C sai
Với ba điểm thẳng hàng phân biệt luôn có hai điểm nằm cùng phía đối với điểm còn lại. Đáp án D đúng
Chọn đáp án D
.JPG)