Tìm một trong các phần bằng nhau của một số

I. KIẾN THỨC CẦN NHỚ

Ví dụ:

$\dfrac{1}{5}$ của $15$ cái bánh bằng bao nhiêu?

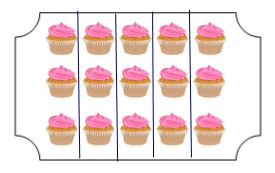
Cách làm:

Chia $15$ cái bánh ra thành $5$ phần bằng nhau. Mỗi phần đó là $\dfrac{1}{5}$ số bánh.

Bài giải:

$\dfrac{1}{5}$của 15 cái bánh là:

$15{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}3$ (cái bánh)

Đáp số: $3$ cái bánh.

II. CÁC DẠNG TOÁN

Dạng 1. Tìm một trong các phần bằng nhau của một số

Muốn tìm một trong các phần bằng nhau của một số ta lấy số đó chia cho số phần bằng nhau.

Ví dụ: \(\dfrac{1}{2}\) của \(12kg\) là bao nhiêu ?

Giải:

Vì \(12:2 = 6\) nên \(\dfrac{1}{2}\) của \(12kg\) bằng \(6kg\)

Dạng 2: Toán đố

Bước 1: Đọc và phân tích kĩ đề, xác định giá trị của số cho trước và số phần bằng nhau.

Bước 2: Muốn tìm một trong các phần bằng nhau của một số thì ta lấy số đó chia cho số phần bằng nhau đã cho.

Bước 3: Trình bày bài giải và kiểm tra lại kết quả vừa tìm được.

Ví dụ: Một cửa hàng có \(36\) bao gạo và đã bán được \(\dfrac{1}{6}\) số bao đó. Hỏi cửa hàng đó đã bán được bao nhiêu bao gạo ?

Phân tích: Muốn tìm \(\dfrac{1}{6}\) của \(36\) bao gạo thì ta cần lấy số bao gạo chia cho \(6\)

Giải:

Cửa hàng đã bán số bao gạo là:

\(36:6 = 6\) (bao)

Đáp số: \(6\) bao.

Dạng 3: So sánh.

Ví dụ:\(\dfrac{1}{2}\) của \(12\) lớn hơn hay nhỏ hơn \(\dfrac{1}{3}\) của \(12\)

Giải:

Ta có:

 \(\dfrac{1}{2}\) của \(12\) có giá trị là: \(12:2 = 6\)

\(\dfrac{1}{3}\) của \(12\) có giá trị là: \(12:3 = 4\) 

Vì \(6 > 4\) nên \(\dfrac{1}{2}\) của \(12\) lớn hơn \(\dfrac{1}{3}\) của \(12\)