Phương pháp giải bài tập định luật Ôm
I- PHƯƠNG PHÁP ĐIỂM NÚT
1. Biểu thức định luật ôm cho đoạn mạch AB
\({I_{AB}} = \frac{{{U_{AB}} + {E_P} - {E_t}}}{{{R_N} + {r_P} + {r_t}}}\)
Trong đó:
+ IAB: cường độ dòng điện qua đoạn AB theo chiều A → B
+ EP: Suất điện động của nguồn phát (V)
+ Et: Suất điện động của nguồn thu (V)
+ rP: điện trở trong của nguồn phát (W)
+ rt: điện trở trong của nguồn thu (W)
+ RN: điện trở tương đương của mạch ngoài (W)
2. Công thức hiệu điện thế giữa hai đầu đoạn mạch AB
\({U_{AB}} = \pm \sum {(E)} \pm I({R_N} + r)\)
Quy ước dấu:
+ Lấy + I nếu dòng I có theo chiều A → B, ngược lại lấy dấu -I
+ Khi đi từ A → B: gặp nguồn nào lấy nguồn đó, gặp cực nào lấy dấu của cực đó.
3. Định lý về nút mạnh (nơi giao nhau của tối thiểu 3 nhánh):
Tại một điểm nút ta luôn có: \(\sum {({I_{den}})} = \sum {({I_{di}})} \)
II- PHƯƠNG PHÁP NGUỒN TƯƠNG ĐƯƠNG
- Bộ nguồn tương đương mắc nối tiếp:
Eb = E1 + E2 + ... + En
rb = r1 + r2 + ... + rn
Có điện trở R ghép nối tiếp với nguồn (e, r) thì:
rb = r1 + r2 + ... + R
Bộ nguồn tương đương của bộ nguồn gồm n nguồn mắc song song
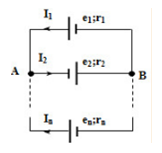
Giả sử bộ nguồn tương đương với một nguồn cực dương tại A, cực âm tại B.
Điện trở tương đương của bộ nguồn: \(\frac{1}{{{r_b}}} = \frac{1}{{{r_1}}} + \frac{1}{{{r_2}}} + ... + \frac{1}{{{r_n}}}\)
Giả sử chiều dòng điện qua các nguồn như hình vẽ (coi các nguồn đều là nguồn phát)
=> \({I_1} = \frac{{{E_1} - {U_{AB}}}}{{{r_1}}};{I_2} = \frac{{{E_2} + {U_{AB}}}}{{{r_2}}},{I_n} = \frac{{{E_1} - {U_{AB}}}}{{{r_1}}}\)
Tại nút A: I2 = I1 + ... + In
\({E_b} = \frac{{\frac{{{E_1}}}{{{r_1}}} - \frac{{{E_2}}}{{{r_2}}} + ... + \frac{{{E_n}}}{{{r_n}}}}}{{\frac{1}{{{r_b}}}}}\)
Quy ước dấu:
Theo chiều ta chọn từ A → B:
+ Nếu gặp cực dương của nguồn trước thì e lấy (+)
+ Nếu gặp cực âm của nguồn trước thì e lấy (-)
+ Nếu tính ra Eb < 0 thì cực của nguồn tương đương ngược với điều giả sử.
+ Nếu tính ra I < 0 thì chiều giả sử dòng điện là sai, ta chọn chiều ngược lại.
