Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x(0\le x\le 3)\) là một hình chữ nhật có hai kích thước là x và \(2\sqrt{9-{{x}^{2}}}.\)
A. 16
B. 17
C. 19
D. 18
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bởi hai mặt phẳng x =a và x = b là \(V=\int\limits_{a}^{b}{S(x)dx}.\)
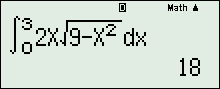
CÂU HỎI CÙNG CHỦ ĐỀ
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x-2y+2z-1=0\). Khoảng cách từ điểm \(A\left( 1;-2;1 \right)\) đến mặt phẳng \(\left( P \right)\) bằng
Cho hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\) liên tục trên đoạn \(\left[ 1;5 \right]\) sao cho \(\int\limits_{1}^{5}{f\left( x \right)\text{d}x}=2\) và \(\int\limits_{1}^{5}{g\left( x \right)\text{d}x}=-4\). Giá trị của \(\int\limits_{1}^{5}{\left[ g\left( x \right)-f\left( x \right) \right]\text{d}x}\) là
Cho số phức z có \(\left| z \right|=2\) thì số phức \(\text{w}=z+3i\) có modun nhỏ nhất và lớn nhất lần lượt là:
Tìm số giá trị nguyên thuộc đoạn \(\left[ -2019\,;2019 \right]\) của tham số \(m\) để đồ thị hàm số \(y=\frac{\sqrt{x-3}}{{{x}^{2}}+x-m}\) có đúng hai đường tiệm cận.
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{x+1}{1}=\frac{z-1}{-1}=\frac{y-3}{2}\). Một vectơ chỉ phương của \(d\) là
Trong hình dưới đây, điểm \(B\) là trung điểm của đoạn thẳng AC. Khẳng định nào sau đây là đúng?
.jpg.png)
Họ nguyên hàm của hàm số \(f(x)=\frac{x+3}{{{x}^{2}}+3\text{x}+2}\) là:
Cho hàm số bậc bốn \(y=f\left( x \right)\) có đồ thị như hình dưới đây. Số nghiệm của phương trình \(3f\left( x \right)+1=0\) là
.jpg.png)
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right)-xf\left( x \right)=0,f\left( x \right)>0,\forall x\in \mathbb{R}\) và \(f\left( 0 \right)=1.\) Giá trị của \(f\left( 1 \right)\) bằng?
Tìm các giá trị của tham số m để hàm số \(y=\frac{1}{2}\ln \left( {{x}^{2}}+4 \right)-mx+3\) nghịch biến trên khoảng \(\left( -\infty ;+\infty \right)\).
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x\left( {2017 + \sqrt {2019 – {x^2}} } \right)\) trên tập xác định của nó. Tính M – m.
Cho không gian Oxyz, cho điểm \(A\left( 0;1;2 \right)\) và hai đường thẳng \({{d}_{1}}:\left\{ \begin{align} & x=1+t \\ & y=-1-2t \\ & z=2+t \\ \end{align} \right.\), \({{d}_{2}}:\frac{x}{2}=\frac{y-1}{1}=\frac{z+1}{-1}\). Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua A và song song với hai đường thẳng \({{d}_{1}},{{d}_{2}}\).
Cho hai số phức z1 = 1+i và z2 = 2-3i. Tính mô đun của số phức z1 + z2
Cho hình lăng trụ \(ABC.{A}'{B}'{C}'\) và M, N là hai điểm lần lượt trên cạnh CA, CB sao cho MN song song với AB và \(\frac{CM}{CA}=k\). Mặt phẳng \(\left( MN{B}'{A}' \right)\) chia khối lăng trụ \(ABC.{A}'{B}'{C}'\) thành hai phần có thể tích \({{V}_{1}}\) (phần chứa điểm C) và \({{V}_{2}}\) sao cho \(\frac{{{V}_{1}}}{{{V}_{2}}}=2\). Khi đó giá trị của k là




