Cho hình nón (N ) có đường kính đáy bằng 4a , đường sinh bằng 5a . Tính diện tích xung quanh của hình nón (N ).

Trong không gian Oxyz , Cho đường thẳng \(\Delta:\left\{\begin{array}{l} x=2+t \\ y=-1-t \\ z=1 \end{array}\right.\).  Véc tơ nào dưới đây là một véc tơ chỉ phương của \(\Delta\)?

Cho hàm số y=f(x)  liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:

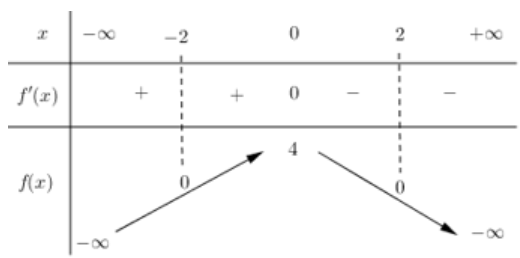
Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?

Cho hai số thực dương x y ; thỏa mãn \(\log _{3} x+x y=\log _{3}(8-y)+x(8-x)\). Giá trị nhỏ nhất của biểu thức \(P=x^{3}-\left(x^{2}+y^{2}\right)-16 x\) bằng?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(S A \perp(A B C D) \text { và } S A=a \sqrt{3}\)  . Khi đó thể tích của hình chóp S.ABCD  bằng:

Với a, b là hai số thực dương khác 1, ta có \(\log _{b^{2}} a\)  bằng

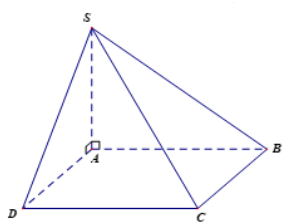
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng (ABCD) và \(SC=a\sqrt3\) (minh họa như hình bên). Góc giữa mặt phẳng (SBC) và và mặt phẳng (ABCD) bằng

Số tiệm cận của đồ thị hàm số \(y=\frac{2 x-3}{x+1}\)là:

Cho cấp số nhân với \(u_1=3\) và \(u_2 = 9\) . Công bội của cấp số nhân đã cho là:

Trong không gian Oxyz, cho điểm \( M(1 ; 2 ; 3) ; N(-1 ; 1 ; 2)\) Phương trình mặt phẳng trung trực của MN là:

Diện tích S của hình phẳng giới hạn bởi các đường \(y=4 x^{2}+x, y=-1, x=0 \text { và } x=1\) được tính bởi công thức nào sau đây?

Xét các số thực a, b thỏa mãn: \(\log _{8}\left(4^{a} . 8^{b}\right)=\log _{4} 16\). Mệnh đề nào dưới đây là đúng?

Giá trị nhỏ nhất của hàm số \(f(x)=x^{4}-6 x^{2}-9\) trên đoạn [-1;4] bằng:

Trong không gian Oxyz  cho điểm \(A(-2 ; 0 ; 1) ; B(0 ; 2 ; 3)\) và mặt phẳng \((P): 2 x+y+z-1=0\). Đường thẳng d qua trung điểm I của AB và vuông góc với mặt phẳng (P) có phương trình là:

Tập nghiệm của bất phương trình \(4^{x}-3.2^{x}+2>0\) là: