Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiCho hàm số \(f(x), \text { có } f\left(\frac{\pi}{2}\right)=0 \text { và } f^{\prime}(x)=\sin x \cdot \cos ^{2} 2 x, \forall x \in \mathbb{R}\). Khi đó \(\int_{0}^{\frac{\pi}{2}} f(x) d x\) bằng:
A. \(-\frac{121}{225}\)
B. \(\frac{2}{232}\)
C. \(-\frac{232}{345}\)
D. \(\frac{92}{232}\)
Lời giải của giáo viên
ToanVN.com
\(\text { Ta có } I=f(x)=\int f^{\prime}(x) d x=\int \sin x \cdot \cos ^{2} 2 x d x=\int \sin x\left(2 \cos ^{2} x-1\right)^{2} d x\)
\(\text { Đặt } t=\cos x \Rightarrow d t=-\sin x d x\)
\(\begin{array}{l} \text { Suy ra } I=-\int\left(2 t^{2}-1\right)^{2} d t=-\int\left(4 t^{4}-4 t^{2}+1\right) d t=-\frac{4}{5} t^{5}+\frac{4}{3} t^{3}-t+c \\ \text { Hay } I=-\frac{4}{5} \cos ^{5} x+\frac{4}{3} \cos ^{3} x-\cos x+C \Rightarrow f(x)=-\frac{4}{5} \cos ^{5} x+\frac{4}{3} \cos ^{3} x-\cos x+C \end{array}\)
\(\text { Mà } f\left(\frac{\pi}{2}\right)=0 \Rightarrow C=0 . \text { Vậy } f(x)=-\frac{4}{5} \cos ^{5} x+\frac{4}{3} \cos ^{3} x-\cos x\)
Tích phân \(J=\int_{0}^{\frac{\pi}{2}} f(x) d x=\int_{0}^{\frac{\pi}{2}}\left(-\frac{4}{5} \cos ^{5} x+\frac{4}{3} \cos ^{3} x-\cos x\right) d x\)
\(\begin{array}{l} =\int_{0}^{\frac{\pi}{2}} \cos x\left(-\frac{4}{5} \cos ^{4} x+\frac{4}{3} \cos ^{2} x-1\right) d x \\ =\int_{0}^{\frac{\pi}{2}} \cos x\left(-\frac{4}{5}\left(1-\sin ^{2} x\right)^{2}+\frac{4}{3}\left(1-\sin ^{2} x\right)-1\right) d x \end{array}\)
\(\begin{array}{l} \text { Đặt } t=\sin x \Rightarrow d t=\cos x d x \\ \text { Đổi cận } x=0 \Rightarrow t=0 ; x=\frac{\pi}{2} \Rightarrow t=1 \end{array}\)
Khi đó \(J=\int_{0}^{1}\left[-\frac{4}{5}\left(1-t^{2}\right)^{2}+\frac{4}{3}\left(1-t^{2}\right)-1\right] d t=-\frac{121}{225}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình nón (N ) có đường kính đáy bằng 4a , đường sinh bằng 5a . Tính diện tích xung quanh của hình nón (N ).
Trong không gian Oxyz , Cho đường thẳng \(\Delta:\left\{\begin{array}{l} x=2+t \\ y=-1-t \\ z=1 \end{array}\right.\). Véc tơ nào dưới đây là một véc tơ chỉ phương của \(\Delta\)?
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:
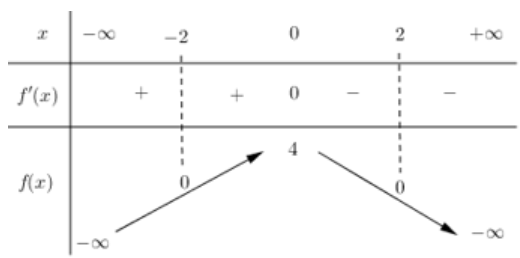
Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(S A \perp(A B C D) \text { và } S A=a \sqrt{3}\) . Khi đó thể tích của hình chóp S.ABCD bằng:
Cho hai số thực dương x y ; thỏa mãn \(\log _{3} x+x y=\log _{3}(8-y)+x(8-x)\). Giá trị nhỏ nhất của biểu thức \(P=x^{3}-\left(x^{2}+y^{2}\right)-16 x\) bằng?
Với a, b là hai số thực dương khác 1, ta có \(\log _{b^{2}} a\) bằng
Số tiệm cận của đồ thị hàm số \(y=\frac{2 x-3}{x+1}\)là:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng (ABCD) và \(SC=a\sqrt3\) (minh họa như hình bên). Góc giữa mặt phẳng (SBC) và và mặt phẳng (ABCD) bằng
Cho cấp số nhân với \(u_1=3\) và \(u_2 = 9\) . Công bội của cấp số nhân đã cho là:
Trong không gian Oxyz, cho điểm \( M(1 ; 2 ; 3) ; N(-1 ; 1 ; 2)\) Phương trình mặt phẳng trung trực của MN là:
Diện tích S của hình phẳng giới hạn bởi các đường \(y=4 x^{2}+x, y=-1, x=0 \text { và } x=1\) được tính bởi công thức nào sau đây?
Xét các số thực a, b thỏa mãn: \(\log _{8}\left(4^{a} . 8^{b}\right)=\log _{4} 16\). Mệnh đề nào dưới đây là đúng?
Giá trị nhỏ nhất của hàm số \(f(x)=x^{4}-6 x^{2}-9\) trên đoạn [-1;4] bằng:
Xét tích phân \(\int_{1}^{e} \frac{1}{x} \ln x d x . \text { Nếu đặt } \ln x=t \text { thì } \int_{1}^{e} \frac{1}{x} \ln x d x\) bằng:
Trong không gian Oxyz cho điểm \(A(-2 ; 0 ; 1) ; B(0 ; 2 ; 3)\) và mặt phẳng \((P): 2 x+y+z-1=0\). Đường thẳng d qua trung điểm I của AB và vuông góc với mặt phẳng (P) có phương trình là:
