Phương pháp giải bài tập vận tốc

1. Nếu hai vật chuyển động ngược chiều

Khi gặp nhau, tổng quãng đường đã đi bằng khoảng cách ban đầu của hai vật.

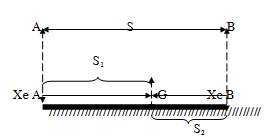
Ta có:

+ \({s_1}\): quãng đường vật A đã tới G

+ \({s_2}\): quãng đường vật B đã tới G

+ \(AB = s = {s_1} + {s_2}\): tổng quãng đường 2 vật đã đi

Tổng quát lại ta có:

\(\left\{ \begin{array}{l}{v_1} = \dfrac{{{s_1}}}{{{t_1}}}\\{v_2} = \dfrac{{{s_2}}}{{{t_2}}}\\s = {s_1} + {s_2}\end{array} \right.;\left\{ \begin{array}{l}{s_1} = {v_1}{t_1}\\{s_2} = {v_2}{t_2}\end{array} \right.;\left\{ \begin{array}{l}{t_1} = \dfrac{{{s_1}}}{{{v_1}}}\\{t_2} = \dfrac{{{s_2}}}{{{v_2}}}\end{array} \right.\)

(Ở đây \(s\) là tổng quãng đường các vật đã đi cũng là khoảng cách ban đầu của hai vật)

Chú ý: Nếu hai vật xuất phát cùng lúc thì thời gian chuyển động của 2 vật cho đến khi gặp nhau bằng nhau: \(t = {t_1} = {t_2}\)

2. Nếu hai vật chuyển động cùng chiều

Khi gặp nhau, hiệu quãng đường các vật đã đi bằng khoảng cách ban đầu giữa hai vật

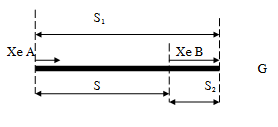
Ta có:

+ \({s_1}\): quãng đường vật A đã tới G

+ \({s_2}\): quãng đường vật B đã tới G

+ \(AB = s = {s_1} + {s_2}\): tổng quãng đường 2 vật đã đi

Tổng quát, ta được:

\(\left\{ \begin{array}{l}{v_1} = \dfrac{{{s_1}}}{{{t_1}}}\\{v_2} = \dfrac{{{s_2}}}{{{t_2}}}\\s = {s_1} - {s_2}{\rm{   }}khi{\rm{   }}\left( {{v_1} > {v_2}} \right)\\s = {s_2} - {s_1}{\rm{   }}khi{\rm{    }}\left( {{v_2} > {v_1}} \right)\end{array} \right.\)

IV - BÀI TOÁN DẠNG CHUYỂN ĐỘNG CỦA THUYỀN KHI XUÔI DÒNG HAY NGƯỢC DÒNG TRÊN HAI BẾN SÔNG

- Khi nước chảy vận tốc thực của canô, xuồng, thuyền, ... lúc xuôi dòng là:

\(v = {v_{can{\rm{o}}}} + {v_{nuoc}}\)   

- Khi nước chảy vận tốc thực của canô, xuồng, thuyền, .. lúc ngược dòng là:

\(v = {v_{can{\rm{o}}}} - {v_{nuoc}}\)

- Khi nước yên lặng: \({v_{nuoc}} = 0\)