Khi tổng hợp hai dao động cùng phương, cùng tần số và khác nhau pha ban đầu thì thấy pha của dao động tổng hợp cùng pha với dao động thứ hai

→ Biên độ của dao động thứ hai lớn hơn biên độ của dao động thứ nhất và hai dao động ngược pha.

Độ dài quỹ đạo dao động của con lắc là:

\(L=2A\Rightarrow A=\frac{L}{2}=\frac{8}{2}=4\left( cm \right)=0,04\left( m \right)\)

Từ đồ thị ta thấy khi động năng bằng 0, thế năng của con lắc:

\({{\text{W}}_{t\max }}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}={{4.10}^{-3}}\left( J \right)\)

\(\Rightarrow \frac{1}{2}0,1.{{\omega }^{2}}.0,{{04}^{2}}={{4.10}^{-3}}\Rightarrow \omega =5\sqrt{2}\left( rad/s \right)\)

Khung xe rung mạnh nhất khi có cộng hưởng

Thời gian xe đi trên mỗi đoạn là:

\(t=T=1,5\left( s \right)\)

\(\Rightarrow v=\frac{s}{t}=\frac{8}{1,5}=5,33\left( m/s \right)=19,2\left( km/h \right)\)

Đơn vị đo của mức cường độ âm là Ben (B).

Góc quét được của vecto quay trong khoảng thời gian \(4,5s\) là:

\(\Delta \varphi =\omega \Delta t=2\pi .4,5=9\pi =\pi \left( rad \right)\)

→ hai thời điểm \({{t}_{1}},{{t}_{2}}\) ngược pha

Li độ của vật ở thời điểm \({{t}_{2}}\) là: \({{x}_{2}}=-{{x}_{1}}=-4\left( cm \right)\)

Để trên dây có sóng dừng, ta có: \(\text{l}=k\frac{\lambda }{2}=k\frac{v}{2f}\Rightarrow f=\frac{kv}{2\text{l}}=\frac{k.40}{2.1,5}=\frac{40}{3}k\)

Theo đề bài ta có: \(30\le f\le 100\Rightarrow 30\le \frac{40}{3}k\le 100\)

\(\Rightarrow 2,25\le k\le 7,5\Rightarrow {{k}_{\max }}=7\)

\(\Rightarrow f=\frac{40}{3}{{k}_{\max }}=\frac{40}{3}.7=93,33\left( Hz \right)\)

Con lắc đơn có quỹ đạo tròn, ở vị trí cân bằng, tổng hợp lực tác dụng lên con lắc bằng lực hướng tâm:

\({{F}_{ht}}=m{{a}_{ht}}=m\frac{{{v}^{2}}}{\text{l}}\to \) A sai

Khi vật nặng ở vị trí biên, động năng của con lắc: \({{W}_{d}}=0\Rightarrow W={{W}_{t}}\to \) B đúng

Dao động của con lắc là dao động điều hòa chỉ khi có biên độ nhỏ → C sai

Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần → D sai

Ta có VTLG:

Từ VTLG ta thấy để vận tốc và li độ cùng dương, vecto quay thuộc góc phần tư thứ IV, góc quét được của vecto quay là: \(\pi <\Delta \varphi <\frac{3\pi }{2}\Rightarrow \pi <5\pi t<\frac{3\pi }{2}\Rightarrow 0,2<t<0,3\left( s \right)\)

Bước sóng là: \(\lambda =\frac{v}{f}=\frac{3}{25}=0,12\left( m \right)=12\left( cm \right)\)

Biên độ dao động của điểm M là:

\({{a}_{M}}=2A\left| \cos \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right|=2A\left| \cos \frac{\pi .\left( 17-15 \right)}{12} \right|=12\)

\(\Rightarrow A=4\sqrt{3}mm\)

Điểm N cách trung điểm O 2 cm, có: 

\(\left\{ \begin{array}{*{35}{l}} AN=10,5cm \\ BN=14,5cm \\ \end{array} \right.\)

Biên độ dao động của điểm N là: \({{a}_{N}}=2A\left| \cos \frac{\pi \left( BN-AN \right)}{\lambda } \right|=2.4\sqrt{3}\left| \cos \frac{\pi .\left( 14,5-10,5 \right)}{12} \right|=4\sqrt{3}\left( mm \right)\)

Cường độ âm: \(I=\frac{P}{4\pi {{r}^{2}}}\Rightarrow I\sim\frac{1}{{{r}^{2}}}\)

\(\Rightarrow \frac{{{I}_{A}}}{{{I}_{B}}}=\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}=4\Rightarrow \frac{{{r}_{2}}}{{{r}_{1}}}=2\)

Tại đầu dây cố định, sóng tới và sóng phản xạ ngược pha nhau: \(\Delta \varphi =\left( 2k+1 \right)\pi \)

Từ phương trình li độ, ta thấy pha ban đầu của dao động là \(-\frac{\pi }{2}rad\)

Nhận xét: Trong 1 chu kì, vật đi qua vị trí \(x=5cm\) 2 lần

Vật qua vị trí \(x=5cm\) lần thứ \(2020\), ta có: \({{t}_{2020}}=1009T+{{t}_{2}}\)

Chu kì dao động là: \(T=\frac{2\pi }{\omega }=\frac{2\pi }{10\pi }=0,2\left( s \right)\)

Ta có VTLG:

Từ VTLG, ta thấy vật qua vị trí \(x=5cm\) lần thứ 2, vecto quay được góc:

\(\Delta \varphi =\frac{\pi }{3}+\frac{\pi }{2}=\frac{5\pi }{6}\left( rad \right)\Rightarrow {{t}_{2}}=\frac{\Delta \varphi }{\omega }=\frac{\frac{5\pi }{6}}{10\pi }=\frac{1}{12}\left( s \right)\)

\(\Rightarrow {{t}_{2020}}=1009T+\frac{1}{12}=\frac{12113}{60}\left( s \right)\)

Khi xách xô nước, để nước không bắn tung tóe ra ngoài người ta thường bỏ một vài chiếc lá vào trong xô nước nhằm mục đích gây ra dao động tắt dần.

Giao thoa hai nguồn cùng pha, tại điểm dao động với biên độ cực đại có hiệu đường đi của sóng từ hai nguồn: \({{d}_{2}}-{{d}_{1}}=k\lambda =2k\frac{\lambda }{2}\)

Hai điểm A, M dao động ngược pha, ta có: \(\Delta \varphi =\frac{2\pi d}{\lambda }=\pi +k2\pi \Rightarrow d=\left( k+0,5 \right)\lambda \)

Động năng của vật bằng 3 lần thế năng của lò xo, ta có:

\({{W}_{d}}=3{{W}_{t}}\Rightarrow {{W}_{d}}=\frac{3}{4}W\) \(\Rightarrow \frac{1}{2}m{{v}^{2}}=\frac{3}{4}.\frac{1}{2}k{{A}^{2}}\Rightarrow v=A\sqrt{\frac{3k}{4m}}\)

Ban đầu vật ở biên dương → pha ban đầu bằng 0

Tần số góc của con lắc là: \(\omega =\sqrt{\frac{g}{\text{l}}}=\sqrt{\frac{{{\pi }^{2}}}{1}}=\pi \left( rad/s \right)\)

Biên độ dài của con lắc là: \({{S}_{0}}=\text{l}{{\alpha }_{0}}=1.0,1=0,1\left( m \right)\)

Phương trình li độ dài của con lắc là: \(S=0,1\cos \pi t\left( m \right)\)

Trên đường nối hai nguồn, khoảng cách giữa hai điểm dao động với biên độ cực đại gần nhau nhất là: \(\frac{\lambda }{2}\)

Sóng dừng hai đầu cố định, trên dây có 1 bụng sóng, ta có: \(\text{l}=\frac{\lambda }{2}=\frac{v}{2f}\Rightarrow f=\frac{v}{2\text{l}}\)

Phương trình truyền sóng tổng quát là: \(u=A\cos \left( 2\pi ft-\frac{2\pi x}{\lambda } \right)\)

Đối chiếu với phương trình sóng, ta có: 

\(\left\{ \begin{array}{*{35}{l}} A=5\left( cm \right) \\ 40\pi =2\pi f\Rightarrow f=20\left( Hz \right) \\ 4\pi =\frac{2\pi }{\lambda }\Rightarrow \lambda =0,5\left( m \right) \\ \end{array} \right.\)

Vận tốc dao động cực đại của phần tử môi trường là: \({{v}_{\max }}=2\pi f.A=2\pi .20.5=200\pi \left( cm/s \right)\)

Vận tốc truyền sóng là: \(v=\lambda f=0,5.20=10\left( m/s \right)\)

Quãng dường sóng truyền được trong \(1s\) là: \(s=v.t=10.1=10\left( m \right)\)

Giữa M và đường trung trực của AB có 2 dãy cực đại → M là cực tiểu thứ \(2\left( k=2 \right)\)

Ta có: \({{d}_{2}}-{{d}_{1}}=\left( k+\frac{1}{2} \right)\lambda \)\(\Rightarrow 20-16=\left( 2+\frac{1}{2} \right)\lambda \Rightarrow \lambda =1,6\left( cm \right)\)

Tốc độ truyền sóng là: \(v=\lambda f=1,6.15=24\left( cm/s \right)\)

Khi vật thực hiện dao động điều hòa với phương trình \({{x}_{1}},{{x}_{2}}\), cơ năng của vật là:

\(\left\{ \begin{array}{*{35}{l}} {{W}_{1}}=\frac{1}{2}m{{\omega }^{2}}{{A}_{1}}^{2} \\ {{W}_{2}}=\frac{1}{2}m{{\omega }^{2}}{{A}_{2}}^{2} \\ \end{array} \right.\)

Theo đề bài ta có: \({{W}_{2}}=4{{W}_{1}}\Rightarrow \frac{1}{2}m{{\omega }^{2}}{{A}_{2}}^{2}=4.\frac{1}{2}m{{\omega }^{2}}{{A}_{1}}^{2}\) \(\Rightarrow {{A}_{2}}^{2}=4{{A}_{1}}^{2}\Rightarrow {{A}_{2}}=2{{A}_{1}}\)

Biên độ dao động tổng hợp của hai dao động là: \(A=\sqrt{{{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos \frac{\pi }{3}}=\sqrt{7}{{A}_{1}}\)

Cơ năng của vật là:

\(W=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\frac{1}{2}m{{\omega }^{2}}.7{{A}_{1}}^{2}=7.\frac{1}{2}m{{\omega }^{2}}{{A}_{1}}^{2}=7{{W}_{1}}\)

Phương trình dao động: \(x=A\cos \left( \omega t+\varphi  \right)\)

Pha dao động là: \(\left( \omega t+\varphi  \right)\) là hàm bậc nhất với thời gian

Ta có hiệu hai mức cường độ âm: \({{L}_{1}}-{{L}_{2}}=\lg \frac{{{I}_{1}}}{{{I}_{2}}}\Rightarrow 12-10=\lg \frac{{{I}_{1}}}{{{I}_{2}}}=2\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}={{10}^{2}}=100\)

Cường độ âm: \(I=\frac{P}{4\pi {{r}^{2}}}\Rightarrow I\sim\frac{1}{{{r}^{2}}}\)

\(\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}=100\Rightarrow \frac{{{r}_{2}}}{{{r}_{1}}}=10\Rightarrow {{r}_{2}}=10{{r}_{1}}=1500\left( m \right)\)

Sóng dừng trên dây có hai đầu cố định, hai tần số liên tiếp tạo ra sóng dừng là:

\(\left\{ \begin{array}{*{35}{l}} {{f}_{1}}=k\frac{v}{2\text{l}} \\ {{f}_{2}}=\left( k+1 \right)\frac{v}{2\text{l}} \\ \end{array} \right.\Rightarrow {{f}_{2}}-{{f}_{1}}=\frac{v}{2\text{l}}\)

\(\Rightarrow 20-15=\frac{v}{2.0,75}\Rightarrow v=7,5\left( m/s \right)=750\left( cm/s \right)\)

Từ phương trình dao động, ta thấy pha ban đầu là 0

Động năng của vật bằng \(\frac{3}{4}\) năng lượng dao động, ta có:

\({{W}_{d}}=\frac{3}{4}W\Rightarrow {{W}_{t}}=\frac{1}{4}W\Rightarrow \frac{1}{2}k{{x}^{2}}=\frac{1}{4}.\frac{1}{2}k{{A}^{2}}\)

\(\Rightarrow {{x}^{2}}=\frac{1}{4}{{A}^{2}}\Rightarrow x=\pm \frac{A}{2}\)

Ta có VTLG:

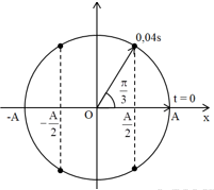
Từ VTLG, ta thấy khi vật qua li độ \(x=\frac{A}{2}\) lần đầu tiên, vecto quay được góc: \(\Delta \varphi =\frac{\pi }{3}\left( rad \right)\)

Tần số góc: \(\omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{\pi }{3}}{0,04}=\frac{25\pi }{3}\left( rad/s \right)\)

\(\Rightarrow T=\frac{2\pi }{\omega }=\frac{2\pi }{\frac{25\pi }{3}}=0,24\left( s \right)\)

Động năng của vật biến thiên với chu kì: \({T}'=\frac{T}{2}=0,12\left( s \right)\)

Khoảng cách giữa hai gợn sóng liên tiếp là: \(\lambda =20\left( cm \right)\)

Vận tốc truyền sóng trên mặt nước là: \(v=\lambda f=20.2=40\left( cm/s \right)\)

Vật dao động cưỡng bức, tần số của vật bằng tần số lực cưỡng bức:

\(\omega =10\pi \left( rad/s \right)\)

\(\Rightarrow \left\{ \begin{array}{*{35}{l}} T=\frac{2\pi }{\omega }=\frac{2\pi }{10\pi }=0,2\left( s \right) \\ f=\frac{\omega }{2\pi }=\frac{10\pi }{2\pi }=5\left( Hz \right) \\ \end{array} \right.\)

Biên độ dao động là: \(A=\frac{L}{2}=\frac{20}{2}=10\left( cm \right)\)

Vật đi được 10cm thì tới vị trí có \(x=5cm\) và chưa đổi chiều → ban đầu vật ở li độ \({{x}_{0}}=-5cm\) và đang đi theo chiều dương.

Ta có VTLG:

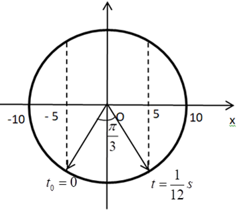
Từ VTLG, ta thấy pha ban đầu của dao động là: \(\varphi =-\frac{2\pi }{3}rad\)

Sau \(\frac{1}{12}s\) kể từ thời điểm ban đầu, vật đi từ li độ \({{x}_{0}}=-5cm\) tới \(x=5cm\), góc quét được là \(\Delta \varphi =\frac{\pi }{3}\).

\(\Rightarrow \omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{\pi }{3}}{\frac{1}{12}}=4\pi \left( rad/s \right)\)

Vậy phương trình dao động của vật là: \(x=10\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm\)

Ban đầu vật có biên độ A và cơ năng \(W=\frac{1}{2}k{{A}^{2}}\)

Sau mỗi chu kì biên độ giảm 2% so với lượng còn lại

⇒ Sau 5 chu kì biên độ dao động của vật lúc này là: \({{A}_{5}}=0,{{98}^{5}}A=0,9039A\)

Năng lượng lúc này của con lắc là: \({{W}_{5}}=\frac{1}{2}kA_{5}^{2}=\frac{1}{2}k.{{\left( 0,9039 \right)}^{2}}{{A}^{2}}=0,817.\frac{1}{2}k{{A}^{2}}\)

\(\Rightarrow {{W}_{5}}=81,7%.W\)

Ta có: \(v=\lambda f\Rightarrow \bar{v}=\bar{\lambda }.\bar{f}=75.440=33000cm/s=330m/s\)

Sai số tuyệt đối của phép đo: \(\Delta v=\bar{v}.\left( \frac{\Delta \lambda }{{\bar{\lambda }}}+\frac{\Delta f}{{\bar{f}}} \right)=330.\left( \frac{1}{75}+\frac{10}{440} \right)=11,9m/s\)

Tốc độ truyền âm tại nơi làm thí nghiệm là: \(330,0\pm 11,9\left( cm/s \right)\)

Bước sóng: \(\lambda =\frac{v}{f}=\frac{300}{10}=30cm\)

Số vân giao thoa cực đại trên đoạn AB bằng só giá trị k nguyên thoả mãn:

\(-\frac{AB}{\lambda }<k<\frac{AB}{\lambda }\Leftrightarrow -\frac{100}{30}<k<\frac{100}{30}\)\(\Leftrightarrow -3,3<k<3,3\Rightarrow k=-3;-2;...;3\)

Để AM nhỏ nhất thì M phải thuộc cực đại ứng với \({{k}_{\max }}=3\) như hình vẽ và thoả mãn:

\({{d}_{2}}-{{d}_{1}}={{k}_{\max }}.\lambda \Leftrightarrow BM-AM=3\lambda =90cm\)

\(\Leftrightarrow \sqrt{A{{B}^{2}}+A{{M}^{2}}}-AM=90\)\(\Leftrightarrow \sqrt{{{100}^{2}}+A{{M}^{2}}}-AM=90\Rightarrow AM=10,56cm\)

Ta có:

\({{v}_{\max }}=\omega A\) \(\Rightarrow A=\frac{{{v}_{\max }}}{\omega }=\frac{1,2\sqrt{3}}{20}=0,06\sqrt{3}m=6\sqrt{3}cm\)

\({{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \)

\(\Leftrightarrow {{\left( 6\sqrt{3} \right)}^{2}}={{6}^{2}}+A_{2}^{2}+2.6.{{A}_{2}}.\cos \left( -\frac{\pi }{6}-\frac{\pi }{2} \right)\)

Lại có biên độ của dao động tổng hợp được xác định bởi công thức:

\({{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \)

\(\Leftrightarrow {{\left( 6\sqrt{3} \right)}^{2}}={{6}^{2}}+A_{2}^{2}+2.6.{{A}_{2}}.\cos \left( -\frac{\pi }{6}-\frac{\pi }{2} \right)\)

\(\Leftrightarrow 108=36+A_{2}^{2}-2{{A}_{2}}\Leftrightarrow A_{2}^{2}-6{{A}_{2}}-72=0\)

\(\Rightarrow {{A}_{2}}=6cm\)

Dây đàn ghi ta hai đầu cố định nên tần số âm cơ bản: \(f=k{{f}_{0}}=k.\frac{v}{2l}\)

Khi dây đàn có chiều dài 0,24m: \({{f}_{1}}=n{{f}_{0}}\Leftrightarrow \frac{v}{2.{{l}_{1}}}=n\frac{v}{2l}\Leftrightarrow \frac{v}{2.0,24}=n\frac{v}{2l}\left( 1 \right)\)

Khi dây đàn có chiều dài 0,2m: \({{f}_{2}}=n{{f}_{0}}\Leftrightarrow \frac{v}{2.{{l}_{2}}}=n\frac{v}{2l}\)\(\Leftrightarrow \frac{v}{2.0,2}=\left( n+1 \right)\frac{v}{2l}=n\frac{v}{2l}+\frac{v}{2l}\left( 2 \right)\)

Từ (1) và (2) suy ra: \(\frac{v}{2.0,2}=\frac{v}{2.0,24}+\frac{v}{2l}\Leftrightarrow \frac{1}{0,4}=\frac{1}{0,48}+\frac{1}{2l}\Rightarrow l=1,2m\)

Biên độ góc: \({{S}_{0}}={{\alpha }_{0}}l=5.\frac{\pi }{180}.81=\frac{20\pi }{9}cm\)

Chu kì dao động: \(T=2\pi \sqrt{\frac{l}{g}}=2\pi \sqrt{\frac{0,81}{{{\pi }^{2}}}}=1,8s\)

Ta có: \(\Delta t=6,9s=6,3+0,6=7.\frac{T}{2}+\frac{T}{3}\)

Quãng đường vật đi được trong \(7.\frac{T}{2}\) là: \({{S}_{\frac{7T}{2}}}=3,5.2A=7.2.\frac{20\pi }{9}=\frac{280\pi }{9}cm\)

Góc quét được trong khoảng \(\frac{T}{3}\) là: \(\alpha =\omega .\frac{T}{3}=\frac{2\pi }{T}.\frac{T}{3}=\frac{2\pi }{3}\)

Biểu diễn trên VTLG ta có :

Từ VTLG \(\Rightarrow {{S}_{\min \frac{T}{3}}}=\frac{{{S}_{0}}}{2}+\frac{{{S}_{0}}}{2}={{S}_{0}}=\frac{20\pi }{9}cm\)

\(\Rightarrow {{S}_{\min 6,9s}}={{S}_{\frac{7T}{2}}}+{{S}_{\min \frac{T}{3}}}=\frac{280\pi }{9}+\frac{20\pi }{9}=\frac{100\pi }{3}\approx 105cm\)

Sử dụng định lí hàm số \(\cos \) trong tam giác ta có:

\(A_{2}^{2}={{A}^{2}}+A_{1}^{2}-2A{{A}_{1}}.cos\left( {{\varphi }_{1}}-\varphi  \right)\)

\(\Leftrightarrow {{5}^{2}}={{\left( 5\sqrt{3} \right)}^{2}}+A_{1}^{2}-2.5\sqrt{3}.{{A}_{1}}.cos\left( \frac{\pi }{2}-\frac{\pi }{3} \right)\)

\(\Leftrightarrow 25=75+A_{1}^{2}-15{{A}_{1}}\Leftrightarrow A_{1}^{2}-15{{A}_{1}}+50=0\)

\(\Leftrightarrow \left( \begin{array}{*{35}{l}} {{A}_{1}}=10cm \\ {{A}_{1}}=5cm \\ \end{array} \right.\)

Từ đồ thị ta thấy:

\(\left\{ \begin{array}{*{35}{l}} {{W}_{d1\max }}=1,5{{W}_{d2\max }}\Leftrightarrow {{m}_{1}}{{\omega }_{1}}A_{1}^{2}=1,5{{m}_{2}}{{\omega }_{2}}A_{2}^{2} \\ {{T}_{d1}}={{T}_{d2}}\Rightarrow {{\omega }_{1}}={{\omega }_{2}} \\ \end{array} \right.\)

\(\Rightarrow {{m}_{1}}A_{1}^{2}=1,5{{m}_{2}}A_{2}^{2}\left( 1 \right)\)

Khi thế năng hai con lắc bằng nhau:

\({{W}_{t1}}={{W}_{t2}}\Leftrightarrow \frac{1}{2}{{m}_{1}}{{\omega }_{1}}x_{1}^{2}=\frac{1}{2}{{m}_{2}}{{\omega }_{2}}x_{2}^{2}\Leftrightarrow {{m}_{1}}x_{1}^{2}={{m}_{2}}x_{2}^{2}\left( 2 \right)\)

Tỉ số động năng của hai con lắc khi đó:

\(\frac{{{W}_{d1}}}{{{W}_{d2}}}=\frac{{{m}_{1}}v_{1}^{2}}{{{m}_{2}}v_{2}^{2}}=\frac{{{m}_{1}}\left( A_{1}^{2}-x_{1}^{2} \right)}{{{m}_{2}}\left( A_{2}^{2}-x_{2}^{2} \right)}=\frac{{{m}_{1}}A_{1}^{2}-{{m}_{1}}x_{1}^{2}}{{{m}_{2}}A_{2}^{2}-{{m}_{2}}x_{2}^{2}}\left( 3 \right)\)

Thay (1); (2) vào (3) ta được:

\(\frac{{{W}_{d1}}}{{{W}_{d2}}}=\frac{1,5{{m}_{2}}A_{2}^{2}-{{m}_{2}}x_{2}^{2}}{{{m}_{2}}A_{2}^{2}-{{m}_{2}}x_{2}^{2}}=\frac{1,5A_{2}^{2}-x_{2}^{2}}{A_{2}^{2}-x_{2}^{2}}=\frac{1,5-\frac{x_{2}^{2}}{A_{2}^{2}}}{1-\frac{x_{2}^{2}}{A_{2}^{2}}}\left( 4 \right)\)

Từ đồ thị ta thấy (1) và (2) dao động vuông pha nên:

\(\frac{x_{1}^{2}}{A_{1}^{2}}+\frac{x_{2}^{2}}{A_{2}^{2}}=1\Leftrightarrow \frac{\frac{{{m}_{2}}x_{2}^{2}}{{{m}_{1}}}}{\frac{1,5{{m}_{2}}A_{2}^{2}}{{{m}_{1}}}}+\frac{x_{2}^{2}}{A_{2}^{2}}=1\)\(\Leftrightarrow \frac{x_{2}^{2}}{1,5A_{2}^{2}}+\frac{x_{2}^{2}}{A_{2}^{2}}=1\Rightarrow \frac{x_{2}^{2}}{A_{2}^{2}}=0,6\left( 5 \right)\)

Từ (4) và (5) \(\Rightarrow \frac{{{W}_{d1}}}{{{W}_{d2}}}=\frac{1,5-0,6}{1-0,6}=\frac{9}{4}\)

Ở VTCB ta có: \({{v}_{0}}=\omega {{\alpha }_{0}}l\Rightarrow \omega =\frac{{{v}_{0}}}{{{\alpha }_{0}}l}=\frac{\frac{1}{3}}{6.\frac{\pi }{180}.1}=\frac{10}{\pi }rad/s\)

Chu kì dao động: \(T=\frac{2\pi }{\omega }=\frac{2\pi }{\frac{10}{\pi }}=\frac{2{{\pi }^{2}}}{10}=\frac{2.10}{10}=2s\)

Bước sóng: \(\lambda =vT=v.\frac{2\pi }{\omega }=1.\frac{2\pi }{20\pi }=0,1m=10cm\)

Công thức tính độ lệch pha: \(\Delta \varphi =\frac{2\pi d}{\lambda }\)

Điểm dao động lệch pha \(\frac{\pi }{6}\) so với nguồn tức là:

\(\Delta \varphi =\frac{\pi }{6}+2k\pi \Leftrightarrow \frac{2\pi d}{\lambda }=\frac{\pi }{6}+2k\pi \)

\(\Rightarrow d=\left( \frac{1}{6}+2k \right)\frac{\lambda }{2}=\left( \frac{1}{6}+2k \right).\frac{10}{2}=\frac{5}{6}+10k\)

Số điểm dao động lệch pha \(\frac{\pi }{6}\) so với nguồn trong khoản O đến M bằng số giá trị k nguyên thỏa mãn:

\(0<d<42,5cm\Leftrightarrow 0<\frac{5}{6}+10k<42,5\)\(\Leftrightarrow -0,08<k<4,17\Rightarrow k=0;1;2;3;4;5\)

Có 5 giá trị k nguyên thỏa mãn ⇒ Có 5 điểm.

Khi có một đàn giao hưởng: \({{I}_{1}}=\frac{P}{4\pi {{R}^{2}}}\Rightarrow {{L}_{1}}=\log \frac{{{I}_{1}}}{{{I}_{0}}}=1,2B\)

Khi có n đàn giao hưởng: \({{I}_{2}}=\frac{nP}{4\pi {{R}^{2}}}\Rightarrow {{L}_{2}}=\log \frac{n{{I}_{1}}}{{{I}_{0}}}=2,376B\)

\(\Rightarrow {{L}_{2}}-{{L}_{1}}=1,176\Leftrightarrow \log n=1,176\Rightarrow n={{10}^{1,176}}=15\)

⇒ Giàn nhạc giao hưởng có 15 người.