Người có thể nghe được âm có tần số từ 16Hz đến 20kHz.

Cho dòng điện một chiều và dòng điện xoay chiều lần lượt đi qua cùng một điện trở thì chúng toả ra nhiệt lượng như nhau là không đúng, vì chưa đề cập tới độ lớn của cường độ dòng điện. Nếu muốn chúng toả ra cùng một nhiệt lượng thì cường độ dòng điện một chiều phải có giá trị bằng giá trị hiệu dụng của dòng điện xoay chiều.

Lực từ tác dụng lên dòng điện có phương vuông góc với mặt phẳng chứa dòng điện và đường cảm ứng từ. 

\(\Rightarrow \) Phát biểu không đúng: Lực từ tác dụng lên dòng điện có phương tiếp tuyến với các đường cảm ứng từ. 

Ta có: \({{P}_{hp}}=\frac{{{P}^{2}}R}{{{U}^{2}}.{{\cos }^{2}}\varphi }\Rightarrow {{P}_{hp}}\sim \frac{1}{{{\cos }^{2}}\varphi }\)

\(\Rightarrow \) Mạch có hệ số công suất càng lớn thì công suất hao phí càng nhỏ.

Tần số dao động điều \(f=3Hz\)

Động năng của con lắc biến thiên theo thời gian với tần số: \({f}'=2f=2.3=6Hz\)

Bước sóng của sóng này được tính bằng công thức:  \(\lambda =\frac{v}{f}\)

Đoạn mạch gồm \({{R}_{1}}\text{ }nt\text{ }{{R}_{2}}\)có: \(\cos \varphi =\frac{R}{Z}=\frac{{{R}_{1}}+{{R}_{2}}}{\sqrt{{{\left( {{R}_{1}}+{{R}_{2}} \right)}^{2}}}}=1\Rightarrow {{(\cos \varphi )}_{\max }}\)

Khi có sóng dừng trên dây, khoảng cách giữa hai bụng liên tiếp bằng một nửa bước sóng.

Ta có: \(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow T\in l,g\)

\(\Rightarrow \)Chu kì dao động điều hòa của con lắc đơn không phụ thuộc vào khối lượng quả nặng.

Chiết suất tỉ đối giữa môi trường khúc xạ với môi trường tới bằng tỉ số giữa chiết suất tuyệt đối của môi trường khúc xạ và chiết suất tuyệt đối của môi trường tới. 

Phương trình dao động điều hòa: \(x=3\cos (4\pi t)cm\)

Pha của dao động tại thời điểm t là: \(4\pi \text{t (rad)}\)

Hai sóng có cùng tần số và có độ lệch pha không đổi theo thời gian là hai sóng kết hợp. 

Hiện tượng cực dương tan xảy ra khi diện phân dung dịch muối kim loại có anốt làm bằng kim loại đó.

Đối với đoạn mạch chỉ chứa tụ điện ta có: 

\(\left\{ \begin{array}{*{35}{l}} {{I}_{0}}=\frac{{{U}_{0}}}{{{Z}_{C}}}=\frac{{{U}_{0}}}{\frac{1}{\omega C}}={{U}_{0}}\omega C \\ {{\varphi }_{i}}={{\varphi }_{u}}+\frac{\pi }{2}=\frac{\pi }{6}+\frac{\pi }{2}=\frac{2\pi }{3} \\ \end{array} \right.\)

Phát biểu không đúng về dao động cơ tắt dần là: Tần số giảm dần theo thời gian.

Ta có công suất hao phí trong quá trình truyền tải điện năng đi xa: \({{P}_{hp}}=\frac{{{P}^{2}}R}{{{U}^{2}}.{{\cos }^{2}}\varphi }\)

Lại có: 

\(R = \frac{{\rho l}}{S} \Rightarrow {P_{hp}} = \frac{{{P^2}}}{{{U^2}.{{\cos }^2}\varphi }}.\frac{{\rho l}}{S} \Rightarrow \left\{ {\begin{array}{*{20}{l}} {{P_{hp}} \sim {P^2}}\\ {{P_{hp}} \sim \;l}\\ {{P_{hp}} \sim \;\frac{1}{{{U^2}}}} \end{array}} \right.\)

Vậy công suất hao phí không tỉ lệ với thời gian truyền điện.

Chu kì trung bình: \(\bar{T}=\frac{2,01+2,12+1,99}{3}=2,04s\)

Sai số tuyệt đối trung bình: \(\overline{\Delta T}=\frac{\left| 2,04-2,01 \right|+\left| 2,04-2,12 \right|+\left| 2,04-1,99 \right|}{3}=0,05s\)

Sai số dụng cụ: \(\Delta {{T}_{dc}}=0,01s\)

Sai số tuyệt đối: \(\Delta T=\overline{\Delta T}+\Delta {{T}_{dc}}=0,05+0,01=0,06s\)

\(\Rightarrow T=(2,04\pm 0,06)s\)  

Pha của dao động tổng hợp:

\(\tan \varphi =\frac{a.\sin \frac{5\pi }{6}+2a.\sin \frac{\pi }{6}}{a.\cos \frac{5\pi }{6}-2a.\cos \frac{\pi }{6}}=-\frac{1}{\sqrt{3}}\Rightarrow \varphi =-\frac{\pi }{6}\)

Độ lệch pha: \(\Delta \varphi =\left| -\frac{\pi }{6}-\frac{\pi }{6} \right|=\frac{\pi }{3}\)

Tần số của dòng điện do máy phát điện xoay chiều một pha tạo ra được tính theo công thức: \(f=n.p\Rightarrow f\sim p\)

\(\Rightarrow \) Để đả bảo được tần số của dòng điện tạo ra người ta thường dùng roto nhiều cặp cực.

Đồng nhất phương trình ta có: 

\(\left\{ \begin{array}{*{35}{l}} \omega =10\pi (rad/s)\Rightarrow f=\frac{\omega }{2\pi }=5Hz \\ \frac{2\pi x}{\lambda }=\pi x\Rightarrow \lambda =2dm=20cm \\ \end{array} \right.\)

Tốc độ truyền sóng: \(v=\lambda f=20.5=100\text{cm/s}\)

Sóng âm truyền nhanh nhất trong sắt. 

Điện áp ở hai đầu cuộn dây khi xảy ra cộng hưởng: \({{U}_{L}}=I.{{Z}_{L}}=\frac{U.{{Z}_{L}}}{R}\)

Khi tăng tần số của dòng điện một lượng nhỏ: \(U_{L}^{\prime }=\frac{U.Z_{L}^{\prime }}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\)

Vậy điện áp ở hai đầu cuộn dây thay đổi. 

\(\Rightarrow \) Kết luận không đúng là điện áp ở hai đầu cuộn dây không đổi.

Giữa S₁ và S₂ có 10 hypebol là quỹ tích của các điểm đứng yên \(\Rightarrow \) có 10 dãy cực tiểu đối xứng nhau qua trung điểm của 2 nguồn.

Khoảng cách giữa 2 cực tiểu liên tiếp là \(\frac{\lambda }{2}\)

\(\Rightarrow \) Khoảng cách giữa 10 cực tiểu liên tiếp là: \((10-1)\frac{\lambda }{2}=13,5cm\Rightarrow \lambda =3cm\)

Tốc độ truyền sóng trên mặt nước: \(v=\lambda f=3.25=75c\text{m/s}=0,75\text{m/s}\)

Thời điểm \({{t}_{1}}:{{i}_{1}}=-2A\) và đang giảm

Thời điểm \(t=t+0,025s\Rightarrow \) Góc quét: \(\alpha =\omega .\Delta t=20\pi .0,025=\frac{\pi }{2}\)

Biểu diễn trên VTLG ta có: 

Từ VTLG ta có tại thời điểm t₂ cường độ dòng điện: \(-2\sqrt{3}A\)

Ở hình A ta có cảm ứng từ \(\overrightarrow{B}\) có chiều hướng từ trong ra ngoài mặt phẳng hình vẽ.

Từ trường \(\overrightarrow{B}\) giảm dần đều \(\Rightarrow \overrightarrow{{{B}_{C}}}\uparrow \downarrow \overrightarrow{B}\)

\(\Rightarrow \overrightarrow{{{B}_{C}}}\) có chiều hướng từ ngoài vào trong

Sử dụng quy tắc nắm tay phải ta xác định được chiều của cường độ dòng điện có chiều cùng chiều kim đồng hồ. 

\(\Rightarrow \) Hình A đúng.

Ta có:

 \(\left\{ \begin{array}{*{35}{l}} {{W}_{d}}={{W}_{t}} \\ W={{W}_{t}}+{{W}_{d}} \\ \end{array}\Rightarrow 2{{W}_{t}}=W\Leftrightarrow 2\cdot \frac{1}{2}k{{x}^{2}}=\frac{1}{2}k{{A}^{2}}\Rightarrow x=\pm \frac{A}{2} \right.\)

Ta có:

\(E=\frac{k.\left| Q \right|}{{{r}^{2}}}\Rightarrow \left| Q \right|=\frac{E.{{r}^{2}}}{k}\Rightarrow \left| Q \right|=\frac{3000.0,{{3}^{2}}}{{{9.10}^{9}}}={{3.10}^{-8}}C\)

Người cận thị đeo kính cận số 2 có nghĩa là độ tụ của kính là: \(D=-2dp\)

\(\Rightarrow \)Tiêu cự của kính: \({{f}_{k}}=\frac{1}{D}=\frac{1}{-2}=-0,5m\)

\(\Rightarrow O{{C}_{v}}=-{{f}_{k}}=0,5m\)

Vậy người đó phải ngồi cách màn hình xa nhất là 0,5m.

Cảm kháng: \({{Z}_{L}}=\omega L=100\pi \cdot \frac{0,2}{\pi }=20\Omega \)

Điện áp cực đại: \({{U}_{0L}}={{I}_{0}}{{Z}_{L}}=4\sqrt{2}.20=80\sqrt{2}V\)

Lại có: \({{\varphi }_{uL}}={{\varphi }_{i}}+\frac{\pi }{2}=-\frac{\pi }{6}+\frac{\pi }{2}=\frac{\pi }{3}\Rightarrow u=80\sqrt{2}.\cos \left( 100\pi t+\frac{\pi }{3} \right)V\)

Ta có giản đồ vecto:

Cuộn dây có điện trở R.

Tam giác OAB vuông tại A nên:

\(AB=\sqrt{O{{A}^{2}}+O{{B}^{2}}}\Leftrightarrow {{U}_{C}}=\sqrt{U_{RL}^{2}+{{U}^{2}}}=\sqrt{{{60}^{2}}+{{80}^{2}}}=100V\)

Cường độ dòng điện hiệu dụng chạy trong mạch: \(I=\frac{{{U}_{C}}}{{{Z}_{C}}}=\frac{100}{50}=2A\)

Có: \(\cos \gamma =\frac{OA}{AB}=\frac{60}{100}=0,6\Rightarrow \gamma ={{53}^{0}}\Rightarrow \alpha ={{90}^{0}}-\gamma ={{37}^{0}}\)

Công suất tiêu thụ của cuộn dây: \(P={{U}_{RL}}.I.\cos \alpha =60.2.\cos 37=96W\)

Ta có: \(\left\{ \begin{array}{*{35}{l}} {{U}_{1}}=220V \\ {{N}_{1}}=1100;{{N}_{2}}=50 \\ {{I}_{1}}=0,032A \\ \end{array} \right.\)

Áp dụng công thức máy biến áp lí tưởng ta có: 

\(\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}=\frac{{{I}_{2}}}{{{I}_{1}}}\Leftrightarrow \frac{220}{{{U}_{2}}}=\frac{1100}{50}=\frac{{{I}_{2}}}{0,032}\Rightarrow {{U}_{2}}=10V;{{I}_{2}}=0,704A\)

Tổng trở của tải tiêu thụ (gồm cuộn dây có điện trở nối tiếp với tụ điện) là: \(Z=\frac{{{U}_{2}}}{{{I}_{2}}}=\frac{10}{0,704}=14,2\Omega \)

Lại có: \(Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\Leftrightarrow 14,{{2}^{2}}={{10}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}\Rightarrow {{Z}_{L}}-{{Z}_{C}}\approx \pm 10\Omega \)

Độ lệch pha giữa u và i: \(\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\frac{\pm 10}{10}=\pm 1\Rightarrow \varphi =\pm \frac{\pi }{4}\)

Vậy độ lệch pha giữa u và i bằng \(\frac{\pi }{4}\) hoặc \(-\frac{\pi }{4}\)

Áp dụng công thức tính chu kì dao động của con lắc đơn ta có:

\(\left\{ \begin{array}{*{35}{l}} {{T}_{1}}=2\pi \sqrt{\frac{{{l}_{1}}}{g}}=1,2s\Rightarrow T_{1}^{2}=4{{\pi }^{2}}.\frac{{{l}_{1}}}{g} \\ {{T}_{2}}=2\pi \sqrt{\frac{{{l}_{2}}}{g}}=1,6s\Rightarrow T_{2}^{2}=4{{\pi }^{2}}.\frac{{{l}_{2}}}{g} \\ T=2\pi \sqrt{\frac{2{{l}_{1}}-{{l}_{2}}}{g}}\Rightarrow {{T}^{2}}=4{{\pi }^{2}}.\frac{2{{l}_{1}}-{{l}_{2}}}{g} \\ \end{array} \right.\)

\(\Rightarrow {{T}^{2}}=2.4{{\pi }^{2}}\frac{{{l}_{1}}}{g}-4{{\pi }^{2}}\frac{{{l}_{2}}}{g}=2T_{1}^{2}-T_{2}^{2}\Rightarrow T=\sqrt{2.1,{{2}^{2}}-1,{{6}^{2}}}\approx 0,57s\)

Bước sóng: \(\lambda =\frac{v}{f}=\frac{340}{680}=0,5m\)

Điều kiện có sóng dừng trên dây hai đầu cố định: \(l=k\frac{\lambda }{2}\Rightarrow k=\frac{2l}{\lambda }=\frac{2.1}{0,5}=4\)

Vậy sóng dừng trên dây với 4 bó sóng. 

Mỗi bó sóng có 2 điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng. 

\(\Rightarrow \) 4 bó sóng có 8 điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng.

Hợp lực cực đại tác dụng vào vật: \({{F}_{\max }}=kA=m{{\omega }^{2}}A\Rightarrow A=\frac{{{F}_{\max }}}{m{{\omega }^{2}}}=\frac{1}{0,{{1.10}^{2}}}=0,1m=10cm\)

Biên độ của dao động tổng hợp: \({{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \)

\(\Leftrightarrow {{10}^{2}}={{6}^{2}}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \frac{\pi }{2}\Leftrightarrow {{10}^{2}}={{6}^{2}}+A_{2}^{2}\Rightarrow {{A}_{2}}=8cm\)

Cường độ dòng điện chạy trong mạch: \(I=0,5A\)

Áp dụng định luật Ôm đối với toàn mạch ta có: \(I=\frac{\xi }{R+r}\Leftrightarrow 0,5=\frac{3}{R+1}\Rightarrow R=5\Omega \)

Chu kì dao động của vật: \(T=\frac{t}{N}=\frac{60}{30}=2s\)

\(\Rightarrow \Delta t=8s=4.2=4T\)

Quãng đường vật đi được trong 1 chu kì là 4A \(\Rightarrow \)Quãng đường vật đi được trong 4 chu kì là 16A

\(\Rightarrow S=16.A=40cm\Rightarrow A=2,5cm\)

\(\Rightarrow \) Chiều dài quỹ đạo: \(L=2A=2.2,5=5cm\)

A,B nằm hai phía so với nguồn âm.

Có \({{L}_{A}}>{{L}_{M}}\Rightarrow OM>OA\Rightarrow \) B và M nằm cùng phía so với nguồn âm. 

M là trung điểm của AB nên: \(OM=AM-OA=\frac{OB+OA}{2}-OA=\frac{OB-OA}{2}\)

\(\Rightarrow OB=2.OM+OA\)

Lại có: \(\left\{ \begin{array}{*{35}{l}} {{L}_{A}}=10.\log \frac{P}{4\pi .O{{A}^{2}}.{{I}_{0}}}=50dB \\ {{L}_{B}}=10.\log \frac{P}{4\pi .O{{B}^{2}}.{{I}_{0}}} \\ {{L}_{M}}=10\cdot \log \frac{P}{4\pi \cdot O{{M}^{2}}\cdot {{I}_{0}}}=47dB \\ \end{array} \right.\)

\(\Rightarrow {{L}_{A}}-{{L}_{M}}=10\log \frac{O{{M}^{2}}}{O{{A}^{2}}}=3\Rightarrow OM=1,4.OA\) \(\Rightarrow OB=2.OM+OA=3,8.OA\)

Lại có: \({{L}_{A}}-{{L}_{B}}=10.\log \frac{O{{B}^{2}}}{O{{A}^{2}}}\Leftrightarrow 50-{{L}_{B}}=20.\log \frac{3,8.OA}{OA}\) \(\Leftrightarrow {{L}_{B}}=50-20.\log 3,8=38,4dB\)

+  Khi \(f={{f}_{1}},\) hệ số công suất của mạch là: \(\cos {{\varphi }_{1}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}^{2}}}}=1\Rightarrow {{Z}_{{{L}_{1}}}}={{Z}_{{{C}_{1}}}}\)

+  Khi \({{f}_{2}}=2{{f}_{1}}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{Z}_{{{L}_{2}}}}=2{{Z}_{{{L}_{1}}}} \\ {{Z}_{{{C}_{2}}}}=\frac{1}{2}{{Z}_{{{C}_{1}}}}=\frac{1}{2}{{Z}_{{{L}_{1}}}} \\ \end{array} \right.\)

Hệ số công suất của mạch là: 

\(\cos {{\varphi }_{2}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}^{2}}}}=0,707=\frac{1}{\sqrt{2}}\)

\(\Rightarrow R={{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}}=2{{Z}_{{{L}_{1}}}}-\frac{1}{2}{{Z}_{{{L}_{1}}}}=\frac{3}{2}{{Z}_{{{L}_{1}}}}=\frac{3}{2}{{Z}_{{{C}_{1}}}}\)

+  Khi \({{f}_{3}}=1,5{{f}_{1}}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{Z}_{{{L}_{3}}}}=\frac{3}{2}{{Z}_{{{L}_{1}}}}=R \\ {{Z}_{{{C}_{3}}}}=\frac{2}{3}{{Z}_{{{C}_{1}}}}=\frac{4}{9}R \\ \end{array} \right.\)

Hệ số công suất của mạch là: 

\(\cos {{\varphi }_{3}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{{{L}_{3}}}}-{{Z}_{{{C}_{3}}}} \right)}^{2}}}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( R-\frac{4}{9}R \right)}^{2}}}}=0,874\)

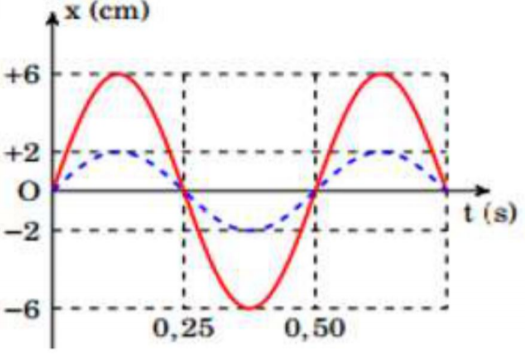
Từ đồ thị ta có: 

+  Chu kì: \(T=0,5s\Rightarrow \omega =\frac{2\pi }{T}=4\pi (ra\text{d/s)}\)

+  Biên độ dao động: \({{A}_{1}}=6cm;{{A}_{2}}=2cm\)

\(\Rightarrow \) Phương trình dao động của hai con lắc lò xo: 

\(\left\{ \begin{array}{*{35}{l}} {{x}_{1}}=6.\cos \left( 4\pi t-\frac{\pi }{2} \right)cm \\ {{x}_{2}}=2.\cos \left( 4\pi t-\frac{\pi }{2} \right)cm \\ \end{array} \right.\)

\(\Rightarrow \frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{A}_{1}}}{{{A}_{2}}}=3\Rightarrow \frac{{{W}_{t1}}}{{{W}_{t2}}}=\frac{x_{1}^{2}}{x_{2}^{2}}=\frac{A_{1}^{2}}{A_{2}^{2}}=9\)

Ở thời điểm t ta có: \(\frac{{{W}_{t1}}}{{{W}_{t2}}}=\frac{{{W}_{1}}-{{W}_{d1}}}{{{W}_{t2}}}=9\Leftrightarrow \frac{\frac{1}{2}m.{{\omega }^{2}}A_{1}^{2}-\frac{1}{2}mv_{1}^{2}}{{{W}_{t2}}}=9\)

\(\Leftrightarrow \frac{\frac{1}{2}.m.{{(4\pi )}^{2}}.0,{{06}^{2}}-\frac{1}{2}.m.0,{{72}^{2}}}{{{4.10}^{-3}}}=9\Rightarrow m=1,25kg=\frac{5}{4}kg\)

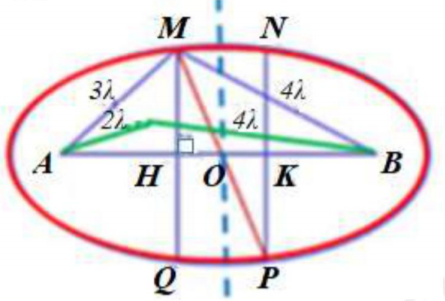
M, N, P, Q thuộc hình chữ nhật, khoảng cách gần nhất bằng độ dài đoạn MN, khoảng cách giữa hai điểm xa nhau nhất bằng độ dài đoạn MP. Ta xét điểm M.

* M dao động với biên độ cực đại: \({{d}_{2}}-{{d}_{1}}=k\lambda \)

* M dao động cùng pha với nguồn: 

+  TH1: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}={{k}_{le}}\lambda \\ {{d}_{2}}+{{d}_{1}}={{n}_{le}}\lambda >5,4\lambda \\ \end{array} \right.\)

+  TH2: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}={{k}_{chan~}}\lambda \\ {{d}_{2}}+{{d}_{1}}={{n}_{chan~}}\lambda >5,4\lambda \\ \end{array} \right.\)

* M gần \(\Delta \) nhất thì

+  TH1: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}=1.\lambda \\ {{d}_{2}}+{{d}_{1}}=7\lambda \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{d}_{1}}=3\lambda =AM \\ {{d}_{2}}=4\lambda =BM \\ \end{array} \right. \right.\)

+  TH2: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}=2.\lambda \\ {{d}_{2}}+{{d}_{1}}=6\lambda \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{d}_{1}}=2\lambda \\ {{d}_{2}}=4\lambda \\ \end{array} \right. \right.\) (loại)

Từ hình vẽ ta có: \(AH+HB=AB\)

\(\Leftrightarrow \sqrt{A{{M}^{2}}-M{{H}^{2}}}+\sqrt{B{{M}^{2}}-M{{H}^{2}}}=AB\)

\(\Leftrightarrow \sqrt{{{(3\lambda )}^{2}}-M{{H}^{2}}}+\sqrt{{{(4\lambda )}^{2}}-M{{H}^{2}}}=5,4\lambda \)

\(\Rightarrow MH=2,189\lambda \Rightarrow AH=\sqrt{A{{M}^{2}}-M{{H}^{2}}}=2,051\lambda \)

\(\Rightarrow HO=AO-AH=\frac{5,4\lambda }{2}-2,051\lambda =0,649\lambda \)

\(\Rightarrow OM=\sqrt{M{{H}^{2}}+O{{H}^{2}}}=2,283\lambda \)

Khoảng cách giữa hai điểm xa nhau nhất có giá trị bằng: \(MP=2.OM=2.2,283\lambda =4,566\lambda \)