Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
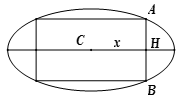
Hỏi bàiTừ một tấm tôn có hình dạng elip với độ dài trục lớn bằng 6 độ dài trục bé bằng 4. Người thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp elíp, sau đó gò tấm tôn hình chữ nhật này thành một hình trụ không có đáy (như hình bên).Tính thể tích lớn nhất có thể thu được của khối trụ đó?
.png)
A. \(V = \frac{{4\sqrt 3 }}{\pi }\)
B. \(V = \frac{{3\sqrt 2 }}{\pi }\)
C. \(V = \frac{{5\sqrt 2 }}{\pi }\)
D. \(V = \frac{{8\sqrt 3 }}{\pi }\)
Lời giải của giáo viên
ToanVN.com
Ta có phương trình đường \(\left( E \right):\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}=1\Rightarrow y=\frac{2}{3}\sqrt{9-{{x}^{2}}}\).
Gọi bán kính đáy hình trụ là r, đường cao là h
Chu vi một đáy của hình trụ là: \(2\pi r=2x\Leftrightarrow r=\frac{x}{\pi }\)
\(AH=\frac{2}{3}\sqrt{9-{{x}^{2}}}\Rightarrow h=2AH=\frac{4}{3}\sqrt{9-{{x}^{2}}}\)
\({{V}_{tru}}=\pi .{{r}^{2}}.h=\pi {{\left( \frac{x}{\pi } \right)}^{2}}.\frac{4}{3}\sqrt{9-{{x}^{2}}}=\frac{4}{3\pi }{{x}^{2}}\sqrt{9-{{x}^{2}}}\)
Đặt \(f\left( x \right)=\frac{4}{3\pi }{{x}^{2}}\sqrt{9-{{x}^{2}}}\,\,\,\left( 0<x<3 \right)\)
\(f'\left( x \right) = \frac{4}{{3\pi }}\left[ {\frac{{18x - 3{x^3}}}{{\sqrt {9 - {x^2}} }}} \right] \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\,(L)\\ x = \sqrt 6 (N)\\ \,x = - \sqrt 6 \,(L) \end{array} \right.\)
Suy ra \({V_{\max }} = \frac{{8\sqrt 3 }}{\pi } \Leftrightarrow x = \sqrt 6 \)
CÂU HỎI CÙNG CHỦ ĐỀ
Tính đường cao h của hình chóp tứ giác đều có cạnh đáy bằng 2a, cạnh bên bằng 3a.
Trong không gian Oxyz cho mặt cầu (S) có tâm I(-1;4;2) và đi qua điểm \(A\left( 1;2;3 \right).\) Khi đó phương trình của mặt cầu (S) là:
Cho cấp số cộng \(\left( {{u}_{n}} \right)\) với \({{u}_{2}}=8\), công sai d=-2. Số hạng đầu của cấp số cộng đã cho bằng
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {{x^2} - 3x + 1}&{khi}&{x \ge 1}\\ {1 + 2x}&{khi}&{x < 1} \end{array}} \right.\).
Tích phân \(I = \int\limits_0^{\frac{\pi }{2}} {f({{\cos }^2}x)\sin 2xdx} + 2\int\limits_0^1 {f(3 - 2x)} dx\) bằng
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và có xét dấu của \({f}'\left( x \right)\) như sau:
.png)
Hàm số đã cho có mấy điểm đại?
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
.PNG)
Hàm số nào dưới đây đồng biến trên khoảng \(\left( -\infty ;+\infty \right)\)?
Tìm nghiệm của bất phương trình: \({\left( {0,5} \right)^{{x^2} - 3x}} < 4\)
Cho hàm số \(y=\left( x-2 \right)\left( {{x}^{2}}+4 \right)\) có đồ thị \(\left( C \right).\) Mệnh đề nào sau đây là đúng?
Cho số phức \(z=a+bi,\left( a,b\in \mathbb{R} \right)\) thỏa mãn điều kiện \(\left| z-3-4i \right|=\sqrt{5}\). Tính giá trị biểu thức P=a+b khi \(\left| z+1-3i \right|+\left| z-1+i \right|\) đạt giá trị lớn nhất.
Với a là số thực dương tùy ý \({a^2}\sqrt {{a^3}} \) bằng
Trong không gian Oxyz cho đường thẳng \(\Delta :\frac{x}{2}=\frac{y-1}{1}=\frac{z+2}{-1}\) và mặt phẳng \(\left( P \right):2x-2y-z+3=0\). Đường thẳng nằm trong \(\left( P \right)\) đồng thời cắt và vuông góc với \(\Delta \) có phương trình là
Thể tích hình chóp có chiều cao là h, diện tích đáy là B bằng
