Trên đoạn mạch không phân nhành có bốn điểm theo đúng thứ tự A, M, N, B. Giữa A và M chỉ có điện trở thuần . Giữa M và N có một hộp kín X. Giữa N và B chỉ có cuộn cảm thuần có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có biểu thức\(u = {U_0}.\cos \left( {\omega t + \varphi } \right)\) . Khi thay đổi L, người ta đo được công suất tiêu thụ của cả đoạn mạch luôn lớn gấp ba lần công suất tiêu thụ của đoạn mạch MB. Biết rằng khi L = 0, độ lệch pha giữa điện áp u và dòng điện trong mạch nhỏ hơn 200. Trong quá trình điều chỉnh L, góc lệch pha giữa điện áp tức thời của đoạn mạch MB so với điện áp tức thời của đoạn mạch Ab đạt giá trị lớn nhất bằng.
A. \(\frac{\pi }{4}\)
B. \(\frac{\pi }{3}\)
C. \(\frac{\pi }{2}\)
D. \(\frac{\pi }{6}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Công suất tiêu thụ của đoạn mạch AB bằng 3 lần của đoạn MB nên ta có:
\(\begin{array}{l}
{P_{AB}} = 3{P_{MB}} \Leftrightarrow {I^2}.(R + {R_X}) = 3.{I^2}.{R_X}\\
\Rightarrow R = 2{R_X}
\end{array}\)
Khi L = 0 thì độ lệch pha giữa điện áp u và dòng điện trong mạch nhỏ hơn 200, vậy trong hộp kín X chỉ có RX
Ta có giản đồ:
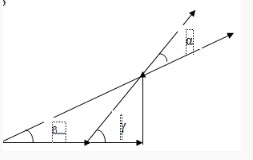
Từ hình vẽ ta thấy góc lệch giữa uMB và uAB là α. Mà α = γ-β
Áp dụng công thức tan của một hiệu ta có:
\(\tan \alpha = \tan (\gamma - \beta ) = \frac{{\tan \gamma - \tan \beta }}{{1 + \tan \gamma .tan\beta }} = \frac{{\frac{L}{{{R_X}}} - \frac{L}{{3{R_X}}}}}{{1 + \frac{L}{{{R_X}}}.\frac{L}{{3{R_X}}}}} = \frac{2}{3}.\frac{{\frac{L}{{{R_X}}}}}{{1 + \frac{{{L^2}}}{{3R_X^2}}}}\)
Đặt \(\frac{L}{{{R_x}}} = x\) ta được
\(\tan \alpha = \frac{2}{3}.\frac{x}{{1 + \frac{{{x^2}}}{3}}}\)
Vì hàm tan là hàm đồng biến nên ta thấy khi α cực đại thì tan α cũng cực đại.
Áp dụng cosi cho biểu thức chứa x ta được:
\(\frac{x}{{1 + \frac{{{x^2}}}{3}}} = \frac{1}{{\frac{1}{x} + \frac{x}{3}}} \le \frac{1}{{2\sqrt {\frac{1}{3}} }}\)
Suy ra:
\(\begin{array}{l}
\tan \alpha \le \frac{2}{3}.\frac{1}{{2.\frac{1}{{\sqrt 3 }}}} = \frac{1}{{\sqrt 3 }}\\
\Rightarrow \alpha \le \frac{\pi }{6}
\end{array}\)
Vậy giá trị cực đại là
\(\frac{\pi }{6}\)
Chọn D
CÂU HỎI CÙNG CHỦ ĐỀ
Một vật dao động điều hòa với phương trình x = 4cosωt (cm). Quãng đường vật đi được trong 2 chu kỳ dao động là
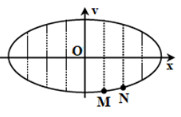
Một vật dao động điều hòa. Hình bên là đồ thị biểu diễn mối quan hệ giữa vận tốc v và li độ x của vật. Gọi k1 và k2 lần lượt là hệ số góc của tiếp tuyến với đồ thị tại M và N. tỷ số \(\frac{{{k_1}}}{{{k_2}}}\) bằng
Một con lắc lò xo gồm lò xo có độ cứng k, vật nặng khối lượng m thực hiện dao động điều hòa. Chu kỳ dao động của con lắc là
Một con lắc lò xo có k = 40N/m và m =100g. Dao động riêng của con lắc này có tần số góc là
Một vật dao động điều hòa vơí phương trình\(x = 5\cos (8t - \frac{\pi }{3})(cm),\) với t tính bằng giây. Tốc độ cực đại của vật trong quá trình dao động là
Sóng ngang truyền trên một sợi dây rất dài từ M đến N rồi đến P với bước sóng λ và chu kỳ T. Biết MN = λ/4; NP = λ/2. Tại thời điểm t1 , M đang có li độ cực tiểu. Khẳng định nào sau đây là sai?
Đặt điện áp xoay chiều \(u = 200\sqrt 2 \cos 100\pi t\) (V) vào hai đầu một đoạn mạch nối tiếp gồm cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}\) (H) và tụ điện có điện dung \(C = \frac{{{{2.10}^{ - 4}}}}{{3\pi }}\) (F). Dùng Ampe kế nhiệt để đo cường độ dòng điện trong mạch. Số chỉ của ampe kế là
Đặt điện áp u = U0 cosωt vào hai bản của tụ điện có điện dung C thì dung kháng của tụ là
Đặt điện áp u = 200cos100πt (V) vào hai đầu đoạn mạch gồm điện trở 100Ω, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết trong đoạn mạch có cộng hưởng điện. Cường độ hiệu dụng của dòng điện trong đoạn mạch là
Trong dao động điều hòa, gia tốc biến đổi điều hòa
Công thức xác định vị trí vân sáng bậc k trong thí nghiệm giao thoa ánh sáng đơn sắc qua khe Young là
Một vật nhỏ khối lượng 1kg dao động điều hòa dưới tác dụng của một lực kéo về có biểu thức F = - 0,8cos(4t) N. Dao động của vật có biên độ
Một dây dẫn thẳng dài đặt trong không khí có dòng điện với cường độ I chạy qua. Độ lớn cảm ứng từ B do dòng điện này gây ra tại một điểm cách dây dẫn một đoạn r được tính bởi công thức
Trong đoạn mạch chỉ có điện trở thuần không đổi, với thời gian như nhau, nếu cường độ dòng điện giảm 2 lần thì nhiệt lượng tỏa ra trên đoạn mạch
Đặt điện áp u = U\(\sqrt{2}\)cosωt (V) vào hai đầu đoạn mạch gồm cuộn cảm thuần mắc nối tiếp với một biến trở R. Ứng với hai giá trị R1= 20Ω và R2 = 80Ω của biến trở thì công suất tiêu thụ trong đoạn mạch đều bằng 400W. Giá trị của U là

