Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
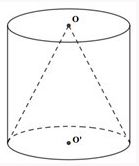
Hỏi bàiMột hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi \({V_1}\) là thể tích của hình trụ, \({V_2}\) là thể tích của hình nón. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\).
A. 2
B. \(2\sqrt 2 \).
C. 3
D. \(\dfrac{1}{3}\).
Lời giải của giáo viên
ToanVN.com
Nhận xét: Hai khối nón và khối trụ có cùng chiều cao \(h\) và cùng bán kính đáy bằng \(r\).
Ta có: \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {r^2}h}}{{\dfrac{1}{3}\pi {r^2}h}} = 3\)
Chọn: C
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right) = 27 + \cos x\) và \(f\left( 0 \right) = 2019\). Mệnh đề nào dưới đây đúng?
Tính thể tích của khối lập phương ABCD.A’B’C’D’ cạnh a.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
Tính thể tích V của khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4\).
Tích \(\dfrac{1}{{2019!}}{\left( {1 - \dfrac{1}{2}} \right)^1}.{\left( {1 - \dfrac{1}{3}} \right)^2}.{\left( {1 - \dfrac{1}{4}} \right)^3}...{\left( {1 - \dfrac{1}{{2019}}} \right)^{2018}}\) được viết dưới dạng \({a^b}\), khi đó \(\left( {a;b} \right)\) là cặp nào trong các cặp sau?
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \(4\pi \). Thể tích khối trụ là
Tìm tọa độ điểm M trên trục Ox cách đều hai điểm \(A\left( {1;2; - 1} \right)\) và điểm \(B\left( {2;1;2} \right)\).
Cho \({\log _3}x = 3{\log _3}2\). Khi đó giá trị của x là
Hỏi có bao nhiêu giá trị m nguyên trong \(\left[ { - 2017;2017} \right]\) để phương trình \(\log \left( {mx} \right) = 2\log \left( {x + 1} \right)\) có nghiệm duy nhất?
Đạo hàm của hàm số \(y = \sin \,x + {\log _3}{x^3}\,\,\left( {x > 0} \right)\) là
Nếu \(\int {f\left( x \right)} dx = \dfrac{{{x^3}}}{3} + {e^x} + C\) thì \(f\left( x \right)\) bằng
Cho hình chóp \(S.\,ABC\) có \(AB = AC = 4,\,BC = 2,\,SA = 4\sqrt 3 \), . Tính thể tích khối chóp \(S.\,ABC.\)
Có bao nhiêu điểm thuộc đồ thị \(\left( C \right)\) của hàm số \(y = \dfrac{2}{{{x^2} + 2x + 2}}\) có hoành độ và tung độ đều là số nguyên?
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = - {x^3} + 2{x^2}\) song song với đường thẳng \(y = x\)?
Gọi \(S = C_n^0 + C_n^1 + C_n^2 + ... + C_n^n\). Giá trị của S là bao nhiêu?
