Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD là hai dây cung của hai đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng
A. \(\frac{5 a^{2}}{4}\)
B. \(\frac{5 a^{2} \sqrt{2}}{4}\)
C. \(5 a^{2}\)
D. \(\frac{5 a^{2}}{2}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
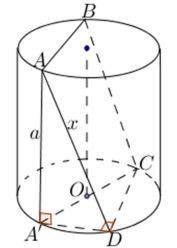
Kẻ đường sinh A A' . Khi đó ta có
\(\left\{\begin{array}{l} C D \perp A D \\ C D \perp A^{\prime} A \end{array} \Rightarrow C D \perp\left(A^{\prime} A D\right) \Rightarrow C D \perp A^{\prime} O \Rightarrow \widehat{A^{\prime} D C}=90^{\circ}\right.\)
Ta có \(\widehat {ADC}\) là góc nội tiếp chắn nửa đường tròn\(\Rightarrow A^{\prime} C=2 a\)
Đặt cạnh hình vuông là x. Khi đó:
\(\left\{\begin{array}{l} A^{\prime} D^{2}=A D^{2}-A^{\prime} A^{2}=x^{2}-a^{2} \\ A^{\prime} D^{2}+D C^{2}=A^{\prime} C^{2} \end{array} \Rightarrow 2 x^{2}-a^{2}=4 a^{2} \Rightarrow x^{2}=S_{A B C D}=\frac{5 a^{2}}{2}\right.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)
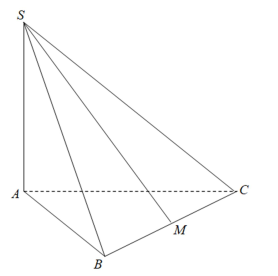
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy, \(S A=\frac{\sqrt{2} a}{2}, A B=A C=a\) . Gọi M là trung điểm của BC ( xem hình vẽ ). Tính góc giữa đường thẳng SM và mặt phẳng (ABC).
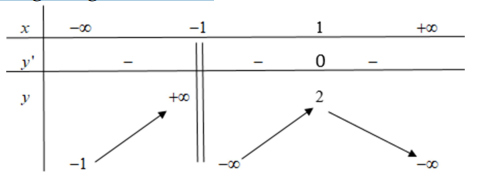
Cho bảng biến thiên của hàm số y =f(x) như hình vẽ. Phát biểu nào sau đây là sai?
Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức \(z=(2+i)^{2}\) có tọa độ là
Trong không gian toạ độ Oxyz, cho đường thẳng\(d:\left\{\begin{array}{l} x=2+3 t \\ y=5-4 t,(t \in \mathbb{R}) \\ z=-6+7 t \end{array}\right.\) và điểm A(1;2;3) . Đường thẳng đi qua A và song song với đường thẳng d có vectơ chỉ phương là:
Cho a và b là hai số thực dương thỏa mãn \(\log _{2}(a b)=\log _{4}\left(a b^{4}\right)\). Mệnh đề nào dưới đây đúng ?
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng \(d: y=-x+m\) cắt đồ thị hàm số \(y=\frac{-2 x+1}{x+1}\) tại hai điểm phân biệt A B , sao cho\(A B \leq 2 \sqrt{2}\). Tổng giá trị các phần tử của S bằng
Tiệm cận ngang của đồ thị hàm số \(y=\frac{5}{x-1}\) là đường thẳng có phương trình
Điểm M trong hình vẽ bên là điểm biểu diễn cho số phức z .
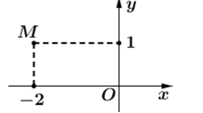
Ký hiệu\(\bar z\) là số phức liên hợp của z . Khi đó mệnh đề nào sau đây là đúng?
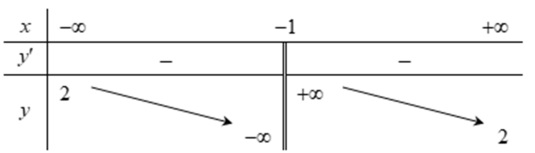
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f'(x) như sau
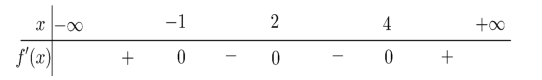
Hàm số y = f(x) có bao nhiêu điểm cực trị?
Cho hàm số y=f(x). Đồ thị hàm số y =f'(x) như hình vẽ. Cho bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) (m là tham số thực). Điều kiện cần và đủ để bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\) là:
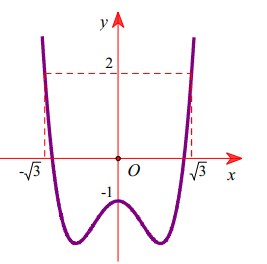
Trong không gian Oxyz, cho mặt phẳng\((P): 5 x-2 y+z+6=0\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P) ?
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a và \(S A \perp(A B C)\), SA=3a . Thể tích của khối chóp S.ABCD là
Tính tích phân \(I=\int\limits_{1}^{e} \frac{\sqrt{1+3 \ln x}}{x} \mathrm{d} x\) bằng cách đặt t\(t=\sqrt{1+3 \ln x}\) . Mệnh đề nào sau đây đúng?
Đồ thị hàm số \(y=f(x)\) với bảng biên thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm cận đứng bằng bao nhiêu?