Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
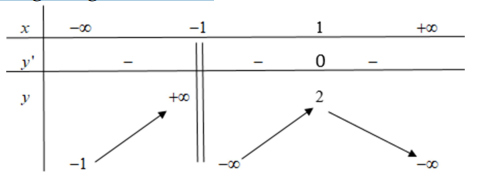
Hỏi bàiCho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA=2a và vuông góc với (ABCD) . Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM.
A. \(d=\frac{a}{3}\)
B. \(d=\frac{a \sqrt{2}}{2}\)
C. \(d=\frac{2 a}{3}\)
D. \(d=\frac{a}{6}\)
Lời giải của giáo viên
ToanVN.com
Gọi \(O=A C \cap B D\)
Vì ABCD là hình vuông cạnh a nên O là trung điểm của BD mà M là trung điểm của SD nên OM// SB / suy ra SB//(ACM).
Do đó \(d(S B, C M)=d(S B,(A C M))=d(B,(A C M))=d(D,(A C M))\)
Gọi H là trung điểm của AD nên \(M H / / S A \Rightarrow M H \perp(A B C D)\)
\(\Rightarrow d(S B, C M)=d(D,(A C M))=2 d(H,(A C M))\)
Kẻ \(H I \perp A C \Rightarrow(M H I) \perp(M A C)\) theo giao tuyến MI.
Kẻ \(H K \perp M I \Rightarrow H K \perp(A C M)\) hay \(d(H,(A C M))=H K\)
Ta có:
\(H I=\frac{1}{2} O D=\frac{1}{4} B D=\frac{1}{4} \sqrt{A B^{2}+A D^{2}}=\frac{a \sqrt{2}}{4}, M H=\frac{1}{2} S A=a\)
suy ra \(\frac{1}{H K^{2}}=\frac{1}{H M^{2}}+\frac{1}{H I^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{1}{a^{2}}+\frac{1}{\left(\frac{a \sqrt{2}}{4}\right)^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{9}{a^{2}} \Leftrightarrow H K=\frac{a}{3}\)
Vậy \(d(S B, C M)=2 d(H,(A C M))=2 H K=\frac{2 a}{3}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)
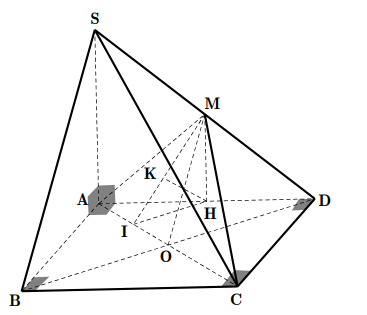
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy, \(S A=\frac{\sqrt{2} a}{2}, A B=A C=a\) . Gọi M là trung điểm của BC ( xem hình vẽ ). Tính góc giữa đường thẳng SM và mặt phẳng (ABC).
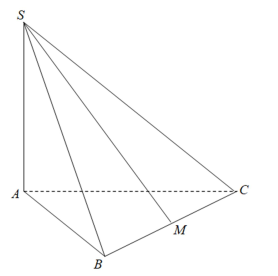
Cho bảng biến thiên của hàm số y =f(x) như hình vẽ. Phát biểu nào sau đây là sai?
Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức \(z=(2+i)^{2}\) có tọa độ là
Cho a và b là hai số thực dương thỏa mãn \(\log _{2}(a b)=\log _{4}\left(a b^{4}\right)\). Mệnh đề nào dưới đây đúng ?
Trong không gian toạ độ Oxyz, cho đường thẳng\(d:\left\{\begin{array}{l} x=2+3 t \\ y=5-4 t,(t \in \mathbb{R}) \\ z=-6+7 t \end{array}\right.\) và điểm A(1;2;3) . Đường thẳng đi qua A và song song với đường thẳng d có vectơ chỉ phương là:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng \(d: y=-x+m\) cắt đồ thị hàm số \(y=\frac{-2 x+1}{x+1}\) tại hai điểm phân biệt A B , sao cho\(A B \leq 2 \sqrt{2}\). Tổng giá trị các phần tử của S bằng
Tiệm cận ngang của đồ thị hàm số \(y=\frac{5}{x-1}\) là đường thẳng có phương trình
Điểm M trong hình vẽ bên là điểm biểu diễn cho số phức z .
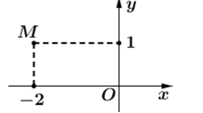
Ký hiệu\(\bar z\) là số phức liên hợp của z . Khi đó mệnh đề nào sau đây là đúng?
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f'(x) như sau
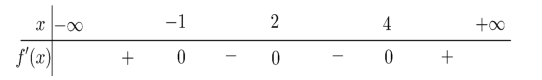
Hàm số y = f(x) có bao nhiêu điểm cực trị?
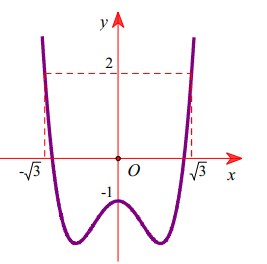
Cho hàm số y=f(x). Đồ thị hàm số y =f'(x) như hình vẽ. Cho bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) (m là tham số thực). Điều kiện cần và đủ để bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\) là:
Trong không gian Oxyz, cho mặt phẳng\((P): 5 x-2 y+z+6=0\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P) ?
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a và \(S A \perp(A B C)\), SA=3a . Thể tích của khối chóp S.ABCD là
Tính tích phân \(I=\int\limits_{1}^{e} \frac{\sqrt{1+3 \ln x}}{x} \mathrm{d} x\) bằng cách đặt t\(t=\sqrt{1+3 \ln x}\) . Mệnh đề nào sau đây đúng?
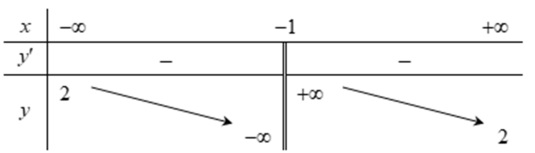
Đồ thị hàm số \(y=f(x)\) với bảng biên thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm cận đứng bằng bao nhiêu?
