Cho hai số phức \({{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}-5+3i \right|=\left| {{z}_{1}}-1-3i \right|,\left| {{z}_{2}}-4-3i \right|=\left| {{z}_{2}}-2+3i \right|\). Giá trị nhỏ nhất của biểu thức \(P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| \overline{{{z}_{1}}}-6+i \right|+\left| {{z}_{2}}-6-i \right|\) là
A. \(2\sqrt {10} .\)
B. 6
C. \(\frac{{16}}{{\sqrt {13} }}.\)
D. \(\frac{{18}}{{\sqrt {13} }}.\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đặt \({{z}_{1}}=x+yi\) thì \(\left| {{z}_{1}}-5+3i \right|=\left| {{z}_{1}}-1-3i \right|\Leftrightarrow 2\text{x}-3y-6=0\left( {{d}_{1}} \right).\)
Đặt \({{z}_{2}}=x'+y'i\) thì \(\left| {{z}_{2}}-4-3i \right|=\left| {{z}_{2}}-2+3i \right|\Leftrightarrow \text{x }\!\!'\!\!\text{ +3}y'-3=0\left( {{d}_{2}} \right).\)
Gọi A,B lần lượt là điểm biểu diễn của \({{z}_{1}},{{z}_{2}}\) thì \(A\in {{d}_{1}};B\in {{d}_{2}}.\)
Gọi \(C\left( 6;1 \right)\).
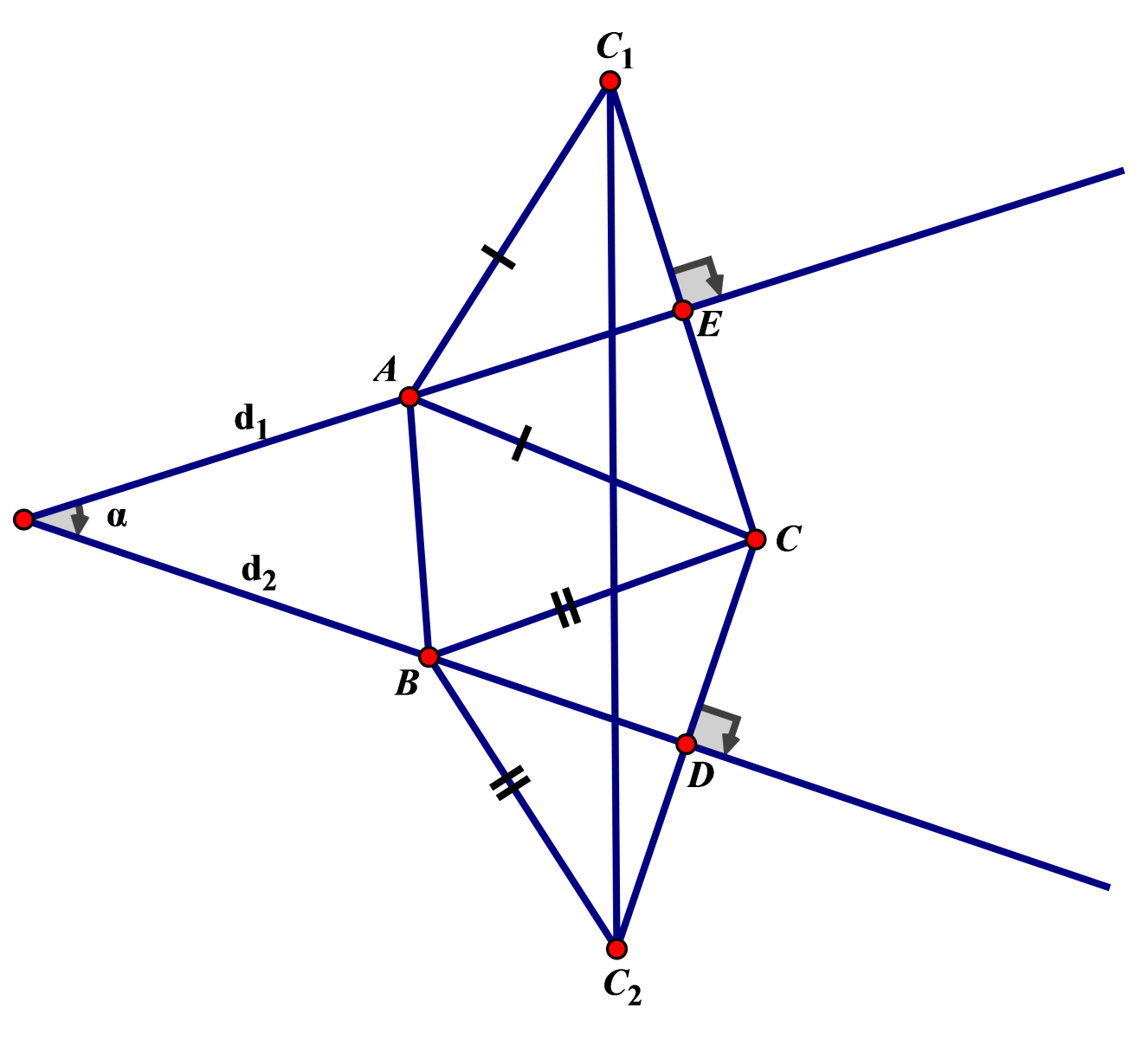
\(\begin{align} & P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| \overline{{{z}_{1}}}-6+i \right|+\left| {{z}_{2}}-6-i \right| \\ & =\left| {{z}_{1}}-{{z}_{2}} \right|+\left| {{z}_{1}}-6-i \right|+\left| {{z}_{2}}-6-i \right|. \\ & =AB+AC+BC\ge {{C}_{1}}{{C}_{2}}. \\ \end{align}\)
Với \({{C}_{1}},{{C}_{2}}\) lần lượt đối xứng với C qua \({{d}_{1}};{{d}_{2}}.\)
Phương trình \(C{{C}_{1}}:3x+2y-20=0\Rightarrow {{C}_{1}}\left( \frac{66}{13};\frac{31}{13} \right)\)
Phương trình \(C{{C}_{2}}:3x-y-17=0\Rightarrow {{C}_{2}}\left( \frac{24}{5};\frac{-13}{5} \right)\)
Vậy \({{C}_{1}}{{C}_{2}}=\frac{18}{\sqrt{13}}.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{1}{\left[ f\left( x \right)+3{{x}^{2}} \right]\text{d}x}=6\). Khi đó \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\) bằng
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm \({f}'\left( x \right)\) như sau:
.png)
Hàm số \(f\left( x \right)\) có bao nhiêu điểm cực trị?
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)=\frac{x+3}{x-1}\) trên đoạn \(\left[ 2;3 \right]\) lần lượt là M và m. Tổng M+m bằng
Nghiệm của phương trình \({{\log }_{3}}\left( 1-3x \right)=2\) là
Với a là số thực dương tùy ý, \(\ln \left( {ea} \right)\) bằng
Cho \(y=f\left( x \right)\) có đồ thị của \(y={f}'\left( x \right)\) như hình vẽ dưới đây.
Đặt \(M=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{max}}}\,\text{ }f\left( x \right), m=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{min}}}\,\text{ }f\left( x \right)\). Giá trị của biểu thức M+m bằng
Tiệm cận đứng của đồ thị hàm số \(y=\frac{-2x+4}{-x+1}\) là đường thẳng:
Trong không gian Oxyz, một véctơ chỉ phương của đường thẳng \(d:\frac{x-2}{-1}=\frac{y-1}{2}=\frac{z}{1}\) là
Cho số phức z=2+3i. Tìm môđun của số phức \(w=\left( 1+i \right)z-\bar{z}\)
Cho hàm số \(f\left( x \right)=-3{{x}^{2}}+1.\) Trong các khẳng định sau, khẳng định nào đúng?
Cho khối chóp S.ABCD có đáy là hình vuông cạnh đáy bằng a và SA vuông góc với đáy với \(SA=a\sqrt{3}.\) Thể tích của khối chóp S.ABCD bằng
Trong không gian Oxyz, cho hai điểm \(A\left( 2;1;1 \right), B\left( 0;3;-1 \right)\). Mặt cầu \(\left( S \right)\) đường kính AB có phương trình là
Với a là số thực dương tùy ý, \(a\sqrt[3]{a}\) bằng
Cho hàm số \(y={{x}^{4}}-3{{x}^{2}}+m\) có đồ thị \(\left( {{C}_{m}} \right)\),với m là tham số thực.Giả sử \(\left( {{C}_{m}} \right)\) cắt trục Ox tại bốn điểm phân biệt như hình vẽ
Gọi \({{S}_{1}},{{S}_{2}},{{S}_{3}}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \({{S}_{1}}+{{S}_{3}}={{S}_{2}}\) là

.PNG)
.PNG)



