Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
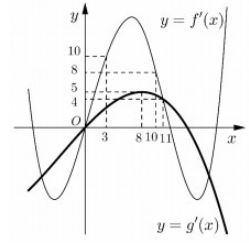
Hỏi bàiCho hai hàm số \(y = f\left( x \right),y = g\left( x \right)\). Hai hàm số \(y = f'\left( x \right),y = g'\left( x \right)\)có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 3} \right) - g\left( {2x - \dfrac{7}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
A. \(\left( {\dfrac{{13}}{4};4} \right)\)
B. \(\left( {7;\dfrac{{29}}{4}} \right)\)
C. \(\left( {6;\dfrac{{36}}{5}} \right)\)
D. \(\left( {\dfrac{{36}}{5}; + \infty } \right)\)
Lời giải của giáo viên
ToanVN.com
Ta có: \(h'\left( x \right) = f'\left( {x + 3} \right) - 2g'\left( {2x - \frac{7}{2}} \right)\)
Để hàm số đồng biến trên
\(\begin{array}{l}\left( {a;b} \right) \Rightarrow h'\left( x \right) > 0\,\,\forall x \in \left( {a;b} \right) \Rightarrow f'\left( {x + 3} \right) > 2g'\left( {2x - \frac{7}{2}} \right)\,\,\forall x \in \left( {a;b} \right)\\ \Rightarrow \mathop {\min }\limits_{\left( {a;b} \right)} f'\left( {x + 3} \right) > 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \frac{7}{2}} \right)\end{array}\)
\(\begin{array}{l}x \in \left( {\dfrac{{13}}{4};4} \right) \Rightarrow \left\{ \begin{array}{l}x + 3 \in \left( {\dfrac{{25}}{4};7} \right) \Rightarrow f'\left( {x + 3} \right) > 10 \Rightarrow \mathop {\min }\limits_{\left( {\dfrac{{13}}{4};6} \right)} f'\left( {x + 3} \right) > 10\\2x - \dfrac{7}{2} \in \left( {3;\dfrac{9}{2}} \right) \Rightarrow g'\left( {2x - \dfrac{7}{2}} \right) < 5 \Rightarrow 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \dfrac{7}{2}} \right) < 10\end{array} \right.\\ \Rightarrow \mathop {\min }\limits_{\left( {a;b} \right)} f'\left( {x + 3} \right) > 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \dfrac{7}{2}} \right)\end{array}\)
\( \Rightarrow \) Hàm số \(y = h\left( x \right)\) đồng biến trên \(\left( {\dfrac{{13}}{4};4} \right)\).
Chọn A.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OA = OB = a và OC = 2a. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng OM và AC bằng
Cho hàm số \(y = \frac{{x - 2}}{{x + 2}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
Từ một hộp chứa 9 quả cầu màu đỏ và 6 quả cầu màu xanh, lấy ngẫu nhiên đồng thời ba quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, \(AC =a\) ; \(BC =\sqrt 2 a\), SA vuông góc với mặt phẳng đáy và \(SA = a\). Góc giữa đường thẳng SB và mặt phẳng đáy bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(\sqrt 3 a\) , SA vuông góc với mặt phẳng đáy và \(SA = a\). Khoảng cách từ A đến mặt phẳng (SBC) bằng
Số tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{\sqrt {x + 25} - 5}}{{{x^2} + x}}\) là
Thể tích của khối trụ tròn xoay có bán kính đáy r và chiều cao h bằng
Từ các chữ số \(1,2,3,4,5,6,7\) lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
.JPG)
Trong không gian Oxyz, mặt phẳng \(\left( P \right):2x + 3y + z-1 = 0\) có một vectơ pháp tuyến là
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 1\) và điểm \(A\left( {2;3;4} \right)\). Xét các điểm M thuộc (S) sao cho đường thẳng AM tiếp xúc với (S), M luôn thuộc mặt phẳng có phương trình là:
Xét các số phức z thỏa mãn \(\left( {\overline z + 2i} \right)\left( {z - 2} \right)\) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
\(\int\limits_1^2 {\dfrac{{dx}}{{3x - 2}}} \) bằng
Cho a > 0, b > 0 thoả mãn \({\log _{4a + 5b + 1}}\left( {16{a^2} + {b^2} + 1} \right) + {\log _{8ab + 1}}\left( {4a + 5b + 1} \right) = 2\). Giá trị của a + 2b bằng
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng \(d:\dfrac{{x + 2}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{2}\) ?
