Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiTrong không gian với hệ tọa độ \({\rm{Ox}}yz\), cho mặt cầu \((S):{x^2} + {y^2} + {z^2} = 9\), điểm \(M(1;1;2)\) và mặt phẳng \((P):x + y + z - 4 = 0\). Gọi \(\Delta \) là đường thẳng đi qua M, thuộc \((P)\) và cắt \((S)\) tại hai điểm A, B sao cho AB nhỏ nhất. Biết rằng \(\Delta \) có một vecto chỉ phương là \(\overrightarrow u (1;a;b)\), tính \(T = a - b.\)
A. \(T = - 2\)
B. \(T = 1\)
C. \(T = - 1\)
D. \(T = 0\)
Lời giải của giáo viên
ToanVN.com
.PNG)
Ta có: \(M \in (P)\)
\(O{M^2} = 6 < {R^2} = 9 \Rightarrow \) M nằm trong mặt cầu \( \Rightarrow \) (P) cắt mặt cầu thành 1 hình tròn (C)
Gọi H là tâm hình tròn (C)
Để AB nhỏ nhất thì \(AB \bot HM\)
Vì \(\left\{ \begin{array}{l}AB \bot HM\\AB \subset (P)\end{array} \right. \Rightarrow \) \(\overrightarrow {{u_{AB}}} = \left[ {\overrightarrow {HM} ,\overrightarrow {{n_{(P)}}} } \right]\)
O là tâm mặt cầu và O(0; 0; 0)
Phương trình OH: \(\left\{ \begin{array}{l}x = t\\y = t\\z = t\end{array} \right.\) \( \Rightarrow H(t;t;t) \in (P) \Rightarrow t = \frac{4}{3}\) \( \Rightarrow H\left( {\frac{4}{3};\frac{4}{3};\frac{4}{3}} \right) \Rightarrow \overrightarrow {HM} = \left( {\frac{{ - 1}}{3};\frac{{ - 1}}{3};\frac{2}{3}} \right)\)
\( \Rightarrow \overrightarrow {{u_{AB}}} = ( - 3;3;0)\) là một vecto chỉ phương của AB
Chọn \(\frac{{ - 1}}{3}\overrightarrow {{u_{AB}}} = (1; - 1;0)\) là vecto chỉ phương của AB
Thì \(a = - 1;b = 0 \Rightarrow a - b = - 1.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + c}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào dưới đây đúng?
.jpg)
Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng \(a\sqrt 2 \). Tính thể tích của khối
nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD.
Trong không gian với hệ tọa độ \({\rm{Ox}}yz,\) cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 + t\\z = 2\end{array} \right.\) và \({d_2}:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{z}{2}\) mặt phẳng \((P):2x + 2y - 3z = 0\). Phương trình nào dưới đây là phương trình mặt phẳng đi qua giao điểm của \({d_1}\) và \((P)\) , đồng thời vuông góc với \({d_2}\)?
Trong không gian với hệ tọa độ \({\rm{Ox}}yz\) cho điểm \(M( - 1;1;3)\) và hai đường thẳng \(\Delta :\frac{{x - 1}}{3} = \frac{{y + 3}}{2} = \frac{{z - 1}}{1},\Delta ':\frac{{x + 1}}{1} = \frac{y}{3} = \frac{z}{{ - 2}}\). Phương trình nào dưới đây là phương trình đường thẳng đi qua\(M\) vuông góc với \(\Delta \) và \(\Delta '.\)
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc \({30^ \circ }\) . Tính thể tích V của khối chóp đã cho.
Tìm giá trị \(m\) nhỏ nhất của hàm số \(y = {x^3} - 7{x^2} + 11x - 2\) trên đoạn [0; 2] .
Cho \(\int\limits_0^6 {f(x)dx = 12} \) . Tính \(I = \int\limits_0^2 {f(3x)dx} .\)
Cho \(F(x) = {x^2}\) là một nguyên hàm của hàm số \(f(x){e^{2x}}\). Tìm nguyên hàm của hàm số \(f'(x){e^{2x}}.\)
Phương trình nào dưới đây nhận hai số phức \(1 + \sqrt 2 i\) và \(1 - \sqrt 2 i\) là nghiệm?
Tìm tập xác định D của hàm số \(y = {(x - 1)^{\frac{1}{3}}}.\)
Cho \({\log _a}x = 3,{\log _b}x = 4\) với \(a,b\) là các số thực lớn hơn 1. Tính \(P = {\log _{ab}}x.\)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
.jpg)
Trong không gian với hệ tọa độ \(Oxyz\) cho điểm \(M(1; - 2;3)\) . Gọi \(I\) là hình chiếu vuông góc của \(M\) trên trục \({\rm{Ox}}\). Phương trình nào dưới đây là phương trình của mặt cầu tâm \(I\) bán kính \(IM\)?
Tìm giá trị thực của tham số \(m\) để phương trình \(\log _3^2x - m{\log _3}x + 2m - 7 = 0\) có hai nghiệm thực \({x_1},{x_2}\) thỏa mãn \({x_1}{x_2} = 81.\)
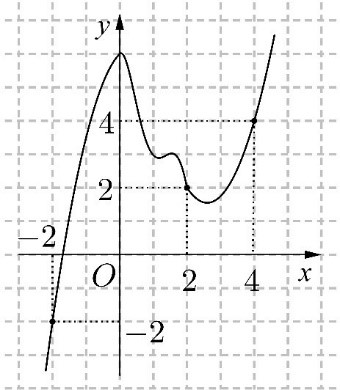
Cho hàm số \(y = f(x)\). Đồ thị của hàm số \(y = f'(x)\) như hình bên. Đặt \(h(x) = 2f(x) - {x^2}\). Mệnh đề nào dưới đây đúng?
