Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiMột hình trụ có bán kính đáy R = 70cm, chiều cao hình trụ h = 20cm. Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?
A. 200cm
B. 100cm
C. 140cm
D. 80cm
Lời giải của giáo viên
ToanVN.com
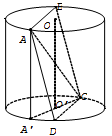
Xét hình vuông ABCD có AD không song song và không vuông góc với trục OO' của hình trụ.
Dựng đường sinh AA', ta có
\(\left\{ \begin{array}{l} CD \bot AA'\\ CD \bot AD \end{array} \right. \Rightarrow CD \bot \left( {AA'D} \right) \Rightarrow CD \bot A'D\)
Suy ra A'C là đường kính đáy nên
\(A'C = 2R = 140{\rm{cm}}{\rm{.}}\)
Xét tam giác vuông AA'C, ta có
\(AC = \sqrt {AA{'^2} + A'{C^2}} = 100\sqrt 2 {\rm{cm}}{\rm{.}}\)
Suy ra cạnh hình vuông bằng 100cm
CÂU HỎI CÙNG CHỦ ĐỀ
Hàm số \(y = \frac{{{x^3}}}{3} - {x^2} + x\) đồng biến trên khoảng nào sau đây?
Cho hai số phức \({z_1} = 1 + 2i;{z_2} = 2 - 3i\). Tổng của hai số phức là
Cho ba điểm \(A,\text{ }B,\text{ }M\) lần lượt là điểm biểu diễn của các số phức \(-4,\,\text{ }4i,\,\text{ }x+3i\). Với giá trị thực nào của x thì \(A,\text{ }B,\text{ }M\) thẳng hàng?
Đồ thị hàm số \(y = {x^3} - 3{x^2} + 2x - 1\) cắt đồ thị hàm số \(y = {x^2} - 3x + 1\) tại hai điểm phân biệt A, B. Khi đó độ dài AB là bao nhiêu ?
Phương trình chính tắc của đường thẳng đi qua điểm \(M\left( 1;-1;2 \right)\) và vuông góc với \(mp\left( \beta \right):2\text{x}+y+3\text{z}-19=0\) là
Môđun của số phức \(z = \frac{{\left( {1 + i} \right)\left( {2 - i} \right)}}{{1 + 2i}}\) là
Biết \(\bar z = {\left( {\sqrt 2 + i} \right)^2}.\left( {1 - \sqrt 2 i} \right)\). Phần ảo của số phức z là
Cần phân công ba bạn từ một tổ có 10 bạn để làm trực nhật. Hỏi có bao nhiêu cách phân công khác nhau?
Trong không gian Oxyz, cho điểm \(A\left( -3;2;-3 \right)\) và hai đường thẳng \({{d}_{1}}:\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-3}{-1}\) và \({{d}_{2}}:\frac{x-3}{1}=\frac{y-1}{2}=\frac{z-5}{3}\). Phương trình mặt phẳng chứa d1 và d2 có dạng
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x - 3y + 4z = 2016\). Véctơ nào sau đây là một véctơ pháp tuyến của mặt phẳng (P) ?
.jpg.png)
Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 2}}\) là
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} - 5}}{{x + 3}}\) trên đoạn [0;2].
Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( { - 3{x^3} + x + 1} \right)\)
