Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
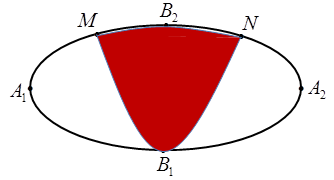
Hỏi bàiMột biển quảng cáo có dạng Elip với bốn đỉnh \({{A}_{1}},{{A}_{2}},{{B}_{1}},{{B}_{2}}\). như hình vẽ. Người ta chia Elip bởi parapol có đỉnh \({{B}_{1}}\), trục đối xứng \({{B}_{1}}{{B}_{2}}\) và đi qua các điểm M, N.Sau đó sơn phần tô đậm với giá 200.000 đồng/\({{m}^{2}}\) và trang trí đèn led phần còn lại với giá 500.000 đồng/\({{m}^{2}}\).Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết \({{A}_{1}}{{A}_{2}}=4m,{{B}_{1}}{{B}_{2}}=2m,\text{ }MN=2m\).
A. 2.760.000 đồng
B. 1.664.000 đồng
C. 2.341.000 đồng
D. 2.057.000 đồng
Lời giải của giáo viên
ToanVN.com
.png)
Phương trình (E)có dạng: \(\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{1}=1\).
Diện tích \(\left( E \right)\) là: \({{S}_{E}}=\pi ab=2\pi \).
Vì MN=2m nên \(M\left( 1;\frac{\sqrt{3}}{2} \right)\).
Vì Parabol có đỉnh \(B\left( 0;-1 \right)\) và đi qua \(M\left( 1;\frac{\sqrt{3}}{2} \right)\) nên \(\left( P \right)\) có phương trình: \(y=\left( \frac{\sqrt{3}}{2}+1 \right){{x}^{2}}-1.\)
Diện tích phần tô đậm giới hạn bởi \(y=\left( \frac{\sqrt{3}}{2}+1 \right){{x}^{2}}-1\) và \(y=\sqrt{1-\frac{{{x}^{2}}}{4}}\) là: \({{S}_{1}}=\int\limits_{-1}^{1}{\left| \left( \sqrt{1-\frac{{{x}^{2}}}{4}} \right)-\left( \frac{\sqrt{3}}{2}+1 \right){{x}^{2}}+1 \right|\text{d}x}\)
Vậy kinh phí cần sử dụng là: \(P={{S}_{1}}.200000+({{S}_{E}}-{{S}_{1}}).500000\approx 2340000\) đồng.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(y=\frac{x-1}{x+2}\). Mệnh đề nào sau đây là mệnh đề đúng?
Cho số phức \(z=5-2i\). Tìm số phức \(w=iz+\overline{z}\).
Giá trị nhỏ nhất của hàm số \(y={{x}^{3}}-2{{x}^{2}}-4x+5\) trên đoạn \(\left[ 1\,;\,3 \right]\) bằng
Diện tích xung quanh của hình trụ có bán kính đáy R=4cm và đường sinh l=5cm bằng:
Tập nghiệm của bất phương trình \({{\left( \frac{1}{1+{{a}^{2}}} \right)}^{2x+1}}>1\) là
Cho hàm số \(f\left( x \right)=\ln \left( {{x}^{4}}+2x \right)\). Đạo hàm \({f}'\left( 1 \right)\) bằng
Trong không gian Oxyz, cho bốn điểm \(A\left( 2\,;\,0\,;\,1 \right), B\left( 3\,;\,1\,;\,5 \right), C\left( 1\,;\,2\,;\,0 \right), D\left( 4\,;\,2\,;\,1 \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua D sao cho ba điểm A, B, C nằm cùng phía đối với \(\left( \alpha \right)\) và tổng khoảng cách từ các điểm A, B, C đến mặt phẳng \(\left( \alpha \right)\) là lớn nhất. Giả sử phương trình \(\left( \alpha \right)\) có dạng: 2x+my+nz-p=0. Khi đó, T=m+n+p bằng:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có một nguyên hàm là \(F\left( x \right)\). Biết \(F\left( 1 \right)=8\), giá trị \(F\left( 9 \right)\) được tính bằng công thức
Tìm tập hợp tất cả các giá trị tham số m để phương trình \({{4}^{{{x}^{2}}-2x+1}}-m{{.2}^{{{x}^{2}}-2x+2}}+3m-2=0\) có 4 nghiệm phân biệt.
Cho hàm số \(y=\frac{3x}{5x-2}\). Khẳng định nào sau đây đúng?
Cho hàm số \(f\left( x \right)={{x}^{4}}\). Hàm số \(g\left( x \right)=f'\left( x \right)-3{{x}^{2}}-6x+1\) đạt cực tiểu, cực đại lần lượt tại \({{x}_{1}},\text{ }{{\text{x}}_{2}}\). Tính \(m=g\left( x{{ }_{1}} \right)g\left( {{x}_{2}} \right)\).
Cho hình chóp tứ giác đều có cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi \(\alpha \) là góc giữa mặt bên và mặt đáy, mệnh đề nào dưới đây đúng?
Điểm \(A\) trong hình bên dưới là điểm biểu diễn số phức \(z\).
.jpg.png)
Mệnh đề nào dưới đây đúng?
Trong không gian Oxyz, mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x+2y+1=0\) có tọa độ tâm I và bán kính R lần lượt là
