Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiCho hàm số \(y=\frac{-x+1}{2 x-1}(C), y=x+m\). Với mọi m đường thẳng ( d) luôn cắt đồ thị (C) tại hai điểm phân biệt A và B . Gọi \(k_{1} ; k_{2}\) , lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B . Giá trị nhỏ nhất của \(T=k_{1}^{2020}+k_{2}^{2020}\) bằng
A. 1
B. 2
C. \(1\over 2\)
D. \(2\over 3\)
Lời giải của giáo viên
ToanVN.com
Phương trình hoành độ giao điểm của hai đồ thị là:
\(\frac{-x+1}{2 x-1}=x+m \Leftrightarrow-x+1=2 x^{2}-x+2 m x-m \Leftrightarrow 2 x^{2}+2 m x-m-1=0\)
phương trình luôn có hai nghiệm phân biệt với mọi m ( vì\(\Delta>0\) ).
Gọi \(A\left(x_{1} ; y_{1}\right) ; B\left(x_{2} ; y_{2}\right)\)
\(\begin{aligned} &\left\{\begin{array}{l} x_{1}+x_{2}=-m \\ x_{1} x_{2}=\frac{-m-1}{2} \end{array}\right.\\ &(C): y=\frac{-x+1}{2 x-1} \Rightarrow y^{\prime}=\frac{-1}{(2 x-1)^{2}} \end{aligned}\)
Ta có:
\(k_{1}^{2020}=\left[\frac{-1}{\left(2 x_{1}-1\right)^{2}}\right]^{2020} ; k_{2}^{2020}=\left[\frac{-1}{\left(2 x_{2}-1\right)^{2}}\right]^{2020}\)
\(T=k_{1}^{2020}+k_{2}^{2020}=\frac{1}{\left(2 x_{1}-1\right)^{4040}}+\frac{1}{\left(2 x_{2}-1\right)^{4040}} \geq 2\left[\frac{1}{\left(2 x_{1}-1\right) \cdot\left(2 x_{2}-1\right)}\right]^{2020}\)
\(\begin{array}{l} \Leftrightarrow T \geq 2\left[\frac{1}{4 x_{1} x_{2}-2\left(x_{1}+x_{2}\right)+1}\right]^{2020} \\ \Leftrightarrow T \geq 2\left[\frac{1}{4 \frac{-m-1}{2}-2(-m)+1}\right]^{2020} \end{array}\)
\(\begin{array}{l} \Leftrightarrow T \geq 2\left[\frac{1}{-2 m-2+2 m+1}\right]^{2020} \\ \Leftrightarrow T \geq 2 \end{array}\)
Dấu = xảy ra khi và chỉ khi
\(\begin{array}{l} \frac{1}{\left(2 x_{1}-1\right)^{4040}}=\frac{1}{\left(2 x_{2}-1\right)^{4040}} \Leftrightarrow\left(2 x_{1}-1\right)^{4040}=\left(2 x_{2}-1\right)^{4040} \\ \Leftrightarrow\left[\begin{array}{l} 2 x_{1}-1=2 x_{2}-1 \\ 2 x_{1}-1=-2 x_{2}+1 \end{array}\right. \end{array}\)
\(\Leftrightarrow\left[\begin{array}{l} x_{1}=x_{2}(V L) \\ x_{1}+x_{2}=1 \Leftrightarrow-m=1 \Leftrightarrow m=-1 \end{array}\right.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số y = f(x)xác định trên \(\mathbb{R} \backslash\{1\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
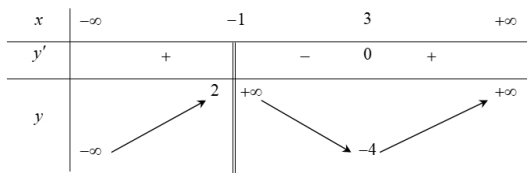
Hàm số \(y=|f(x)|\)có bao nhiêu điểm cực trị?
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { cạnh } 2 a\) . Gọi M là trung điểm của BB′ và P thuộc cạnh DD′ sao cho \(D P=\frac{1}{4} D D^{\prime}\). Biết mặt phẳng ( AMP) cắt CC′ tại N , thể tích của khối đa diện AMNPBCD bằng
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D ,\(S A \perp(A B C D)\) . Góc giữa SB và mặt phẳng đáy bằng 45°, E là trung điểm của SD , \(A B=2 a, A D=D C=a\) . Tính khoảng cách từ B đến ( ACE) .
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
Từ các chữ số 1,5,6,7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau?
Tìm nghiệm của phương trình \(\log _{9}(x+1)=\frac{1}{2}\)
Cho các số thực a , b thỏa mãn điều kiện \(0<b<a<1\) . Tìm giá trị nhỏ nhất của biểu thức \(P=\log _{a} \frac{4(3 b-1)}{9}+8\left(\log _{\frac{b}{a}} a\right)^{2}-1\)
Giải bất phương trình \((7+4 \sqrt{3})^{x-1}<7-4 \sqrt{3}\)
Cho số phức z thỏa mãn điều kiện \((1+i) \bar{z}-1-3 i=0\) . Tìm phần ảo của số phức
Gọi \(x_{1}, x_{2} \) là hai nghiệm nguyên dương của bất phương trình \(\log _{2}(1+x)<2\) . Tính giá trị của \(P=x_{1}+x_{2}\)
Cho tứ diện \(S . A B C \text { có } S A=S B=S C=A B=A C=a ; B C=a \sqrt{2}\) . Góc giữa hai đường thẳng AB và SC bằng
Tìm tập xác định D của hàm số \(y=\left(x^{2}-2 x+1\right)^{\frac{1}{3}}\)
Cho hàm số y =f(x) có bảng biến thiên của đạo hàm y ' như sau:
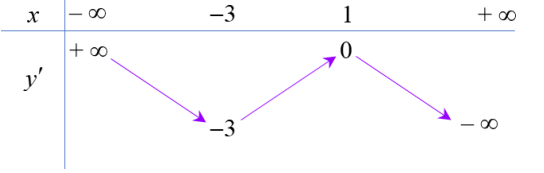
Bất phương trình \(f(x)<\mathrm{e}^{x}+m\) đúng với mọi \(x \in(-1 ; 1)\)khi và chỉ khi
Gọi R là bán kính, S là diện tích mặt cầu và V là thể tích của khối cầu. Công thức nào sau đây sai?
