Trong không gian Oxyz, cho \(A\left( {1;3;5} \right),\,\,B\left( { - 5; - 3; - 1} \right)\). Phương trình mặt cầu đường kính AB là: 

Cho tứ diện ABCD có \(AB = AC,\,\,BD = DC\). Khẳng định nào sau đây đúng?

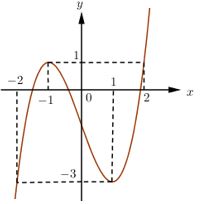
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như ở hình vẽ bên. Phương trình \(f\left( {f\left( x \right) - 1} \right) = 0\) có tất cả bao nhiêu nghiệm thực phân biệt ? 

Trong không gian \(Oxyz\) cho điểm \(I\left( {2;\,3;\,4} \right)\) và \(A\left( {1;\,2;\,3} \right).\) Phương trình mặt cầu tâm \(I\) và đi qua \(A\) có phương trình là: 

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = \left( {2x + 1} \right)\left( {x - 3} \right){\left( {x + 5} \right)^4}.\) Hàm số đã cho có tất cả bao nhiêu điểm cực trị?

Có tất cả bao nhiêu giá trị nguyên của \(m\) để hàm số \(y = \dfrac{{x + 2}}{{x + 3m}}\) đồng biến trên \(\left( { - \infty ; - 6} \right)?\) 

Cho mặt cầu \(S\left( {O;R} \right)\) và mặt phẳng \(\left( \alpha  \right)\). Biết khoảng cách từ O tới  \(\left( \alpha  \right)\) bằng d. Nếu \(d < R\) thì giao tuyến của mặt phẳng \(\left( \alpha  \right)\) với mặt cầu \(S\left( {O;R} \right)\) là đường tròn có bán kính bằng 

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào sau đây: 

Đường cong trong hình vẽ bên là đồ thị của 1 trong 4 hàm số dưới đây, đó là hàm số nào?

Trong không gian \(Oxyz\) cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 2 = 0\) và mặt phẳng \(\left( \alpha  \right):\,\,4x + 3y - 12z + 10 = 0.\) Lập phương trình mặt phẳng \(\left( \beta  \right)\) thỏa mãn đồng thời các điều kiện: Tiếp xúc với \(\left( S \right),\) song song với \(\left( \alpha  \right)\) và cắt trục \(Oz\) ở điểm có cao độ dương. 

Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;\,6} \right],\) có đồ thị hàm số như hình vẽ. Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(f\left( x \right)\) trên miền \(\left[ { - 2;\,6} \right].\) Tính giá trị của biểu thức \(T = 2M + 3m.\)

Hệ số \({x^6}\) khi khai triển đa thức \(P\left( x \right) = {\left( {5 - 3x} \right)^{10}}\) có giá trị bằng đại lượng nào sau đây? 

Giới hạn \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{{5x - 3}}{{1 - 2x}}\) bằng số nào sau đây?  

Cho \(\int\limits_0^1 {f\left( x \right)dx}  = 3,\,\,\int\limits_0^1 {g\left( x \right)dx}  =  - 2\). Tính giá trị của biểu thức \(I = \int\limits_0^1 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx} \). 

Một khối trụ bán kính đáy là \(a\sqrt 3 ,\) chiều cao là \(2a\sqrt 3 .\) Tính thể tích khối cầu ngoại tiếp khối trụ.