Tìm tất cả các giá trị của tham số để hàm số \(y = {\log _2}\left( {{x^2} - 2x + m} \right)\) có tập xác định là R.

Tính giá trị của biểu thức \(P = \log \left( {\tan 1^\circ } \right) + \log \left( {\tan 2^\circ } \right) + \log \left( {\tan 3^\circ } \right) + ... + \log \left( {\tan 89^\circ } \right)\).

Số các giá trị nguyên của tham số \(m\) để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) có hai nghiệm phân biệt là:

Giải phương trình \({\left( {2,5} \right)^{5x - 7}} = {\left( {\frac{2}{5}} \right)^{x + 1}}\).

Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \frac{{m\ln x - 2}}{{\ln x - m - 1}}\) nghịch biến trên \(\left( {{e^2}; + \infty } \right)\).

Cho 2 số thực dương \(a, b\) thỏa mãn \(\sqrt a  \ne b,a \ne 1,{\log _a}b = 2\). Tính \(T = {\log _{\frac{{\sqrt a }}{b}}}\sqrt[3]{{ba}}\).

Cho hàm số \(y=a^x\) với \(0 < a \ne 1\) có đồ thị (C). Chọn khẳng định sai?

Gọi \(a\) là một nghiệm của phương trình \({\left( {26 + 15\sqrt 3 } \right)^x} + 2{\left( {7 + 4\sqrt 3 } \right)^x} - 2{\left( {2 - \sqrt 3 } \right)^x} = 1\). Khi đó giá trị của biểu thức nào sau đây là đúng?

Chọn ngẫu nhiên một số tự nhiên A có bốn chữ số. Gọi N là số thỏa mãn \(3^N=A\). Xác suất để N là số tự nhiên bằng:

Cho \(a = {\log _2}5,b = {\log _3}5\). Tính \({\log _{24}}600\) theo \(a, b\).

Đặt \(a = {\log _2}3,b = {\log _2}5,c = {\log _2}7\). Biểu thức biểu diễn \({\log _{60}}1050\) theo \(a, b, c\) là.

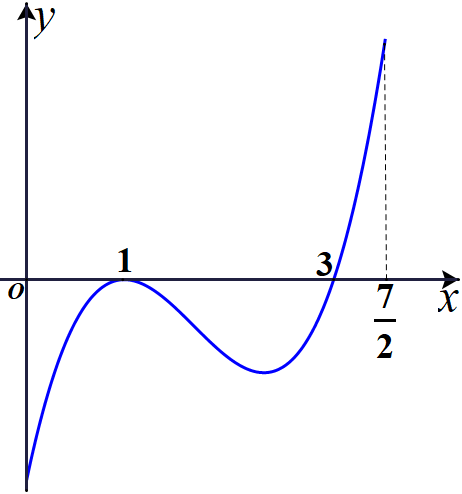
Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f'(x)\) như hình vẽ. Hỏi hàm số \(y=f(x)\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;\frac{7}{2}} \right]\) tại điểm \(x_0\) nào dưới đây?

Gọi \(x, y\) là các số thực dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}\left( {x + y} \right)\) và \(\frac{x}{y} = \frac{{ - a + \sqrt b }}{2}\), với \(a, b\) là hai số nguyên dương. Tính \(a+b\).

Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} - 3x + 1} \right) \le 0\) là

Cho hàm số \(y = {x^3} - {x^2} + 2x + 5\) có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là